Question

已知α∈(0,π),求证:2sin2α≤.

Answer 1

证法一：(作差比较法)

2sin2α

∵α∈(0,π),

∴sinα＞0,1-cosα＞0,(2cosα-1)²≥0.

∴2sin2α≤0.

∴2sin2α≤.

证法二：(作商比较法)

∵0＜α＜π,∴sinα＞0,1-cosα＞0.

∴＞0.

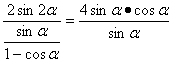·(1-cosα)

=4cosα(1-cosα)

=1-(2cosα-1)²≤1,

∴2sin2α≤.

证法三:(分析法)

要证明2sin2α≤成立,

只要证明4sinαcosα≤.

∵α∈(0,π),∴sinα＞0.

只要证明4cosα≤.

上式可变形为4≤+4(1-cosα).

∵1-cosα＞0,

∴+4(1-cosα)≥=4,

当且仅当cosα=,即α=时取等号.

∴4≤+4(1-cosα)成立.

∴不等式2sin2α≤成立.

证法四:(综合法)

∵+4(1-cosα)≥4,

(1-cosα＞0,当且仅当cosα=即α=时,取等号)

∴4cosα≤.

∵α∈(0,π),∴sinα＞0.

∴4sinαcosα≤.

∴2sin2α≤.