Question

已知函数y=f（x）=-x³+ax²+b…（a，b∈R）．
（Ⅰ）当a＞0时，若f（x）满足：y_极小值=1，y_极大值=

31

27

，试求f（x）的解析式；
（Ⅱ）若x∈[0，1]时，y=f（x）图象上的任意一点处的切线斜率k满足：|k|≤1，求a的取值范围．

Answer 1

分析：（Ⅰ）求出导函数的根，列出x，f′（x），f（x）d的变化的表格，根据极值的定义求出极值，列出方程求出解析式．
（Ⅱ）根据导数的几何意义：函数在切点处的导数值是切线的斜率，列出不等式；分离参数，通过求函数的最值，求出不等式恒成立时的参数范围．

解答：解：：（Ⅰ）f′（x）=-3x²+2ax=0得x=0或x=

2

3

a．
a＞0时，x变化时f'（x），f（x）变化如下表：

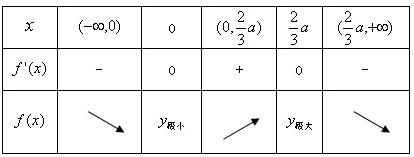
所以f（0）=b=1，f(

2

3

a)=-

8

27

a3+a•

4

9

a2+1=

31

27

，
即a=1，b=1．故f（x）=-x³+x²+1；
（Ⅱ）由题设x∈[0，1]时，恒有|k|=|f′（x）|≤1，
即-1≤-3x²+2ax≤1在x∈[0，1]上恒成立．
当x=0时，a∈R；
当x∈（0，1]时，由-3x²+2ax≥-1恒成立，
即2ax≥3x²-1，a≥

1

2

(3x-

1

x

)，
所以a≥1（函数

1

2

(3x-

1

x

)在（0，1]上为增函数）．
另一方面，由-3x²+2ax≤1恒成立，a≤

1

2

(3x+

1

x

)，
所以a≤

3

（当且仅当x=

3

3

时，取最值）．
综上所述：1≤a≤

3

．

点评：本题考查利用导数求函数的极值、导数的几何意义、通过分离参数求函数的最值求出不等式恒成立的参数范围．