题目内容
如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4 的平行四边形MNEF.平面上的动点G满足|
的平行四边形MNEF.平面上的动点G满足| |=2(O为坐标原点)
|=2(O为坐标原点)(I)求点E、M所在曲线C1的方程及动点G的轨迹C2的方程;
(Ⅱ)已知过点F的直线l交曲线C1于点P、Q,交轨迹C2于点A、B,若|
 |∈(
|∈( ),求△NPQ内切圆的半径的取值范围.
),求△NPQ内切圆的半径的取值范围.
【答案】分析:(I)根据椭圆的定义,可得曲线C1是以F、N为焦点的椭圆,由题中数据即可求出曲线C1的方程为 +y2=1;再由圆的定义即可得到动点G的轨迹C2的方程为x2+y2=4;
+y2=1;再由圆的定义即可得到动点G的轨迹C2的方程为x2+y2=4;
(II)由题意得直线l与x轴不垂直,设l方程为y=k(x+1),利用点到直线的距离公式结合垂径定理,算出|AB|=2 .设P(x1,y1)、Q(x2,y2),△NPQ内切圆半径r满足
.设P(x1,y1)、Q(x2,y2),△NPQ内切圆半径r满足 |NF|•|y1-y2|=
|NF|•|y1-y2|= •r•(|PN|+|PQ|+|QN|),结合题中数据得到r=
•r•(|PN|+|PQ|+|QN|),结合题中数据得到r= |y1-y2|,由直线方程与椭圆消去x,得关于y的二次方程,再利用根与系数的关系算出|y1-y2|关于k的式子,从而得到r关于k的函数关系式,结合函数的单调性讨论可得r的取值范围.
|y1-y2|,由直线方程与椭圆消去x,得关于y的二次方程,再利用根与系数的关系算出|y1-y2|关于k的式子,从而得到r关于k的函数关系式,结合函数的单调性讨论可得r的取值范围.
解答:解:(I)∵四边形MNEF是平行四边形,周长为4
∴点E到点F、N的距离之和等于2 (定长),且|NF|=2<2
(定长),且|NF|=2<2
由椭圆的定义,得曲线C1的方程为 +
+ =1(a>b>0)
=1(a>b>0)
可得a= ,c=1,b2=a2-c2=1,
,c=1,b2=a2-c2=1,
∴曲线C1的方程为 +y2=1
+y2=1
∵| |=2,∴动点G的轨迹为以原点为圆心,半径为2的圆
|=2,∴动点G的轨迹为以原点为圆心,半径为2的圆
即曲线C2的方程为x2+y2=4;
(II)当l垂直x轴时,令x=-1代入曲线C2的方程得y=
∴|AB|=2 ∉(
∉( ),不符合题意
),不符合题意
因此直线l与x轴不垂直,设l方程为y=k(x+1)
原点到直线l的距离为d= ,
,
由圆的几何性质,得到|AB|=2 =2
=2 =2
=2
由|AB|∈( ),解之得k2>
),解之得k2>
联解 ,消去x得(2+
,消去x得(2+ )y2-
)y2- y-1=0
y-1=0
设P(x1,y1),Q(x2,y2),△NPQ内切圆的半径为r
可得y1+y2= =
= ,y1y2=-
,y1y2=- =-
=-
∵ |NF|•|y1-y2|=
|NF|•|y1-y2|= •r•(|PN|+|PQ|+|QN|),其中|NF|=2,|PN|+|PQ|+|QN|=4
•r•(|PN|+|PQ|+|QN|),其中|NF|=2,|PN|+|PQ|+|QN|=4
∴r= |y1-y2|
|y1-y2|
而|y1-y2|= =
= =
=
∵ ,∴1-
,∴1-

别处,因为1- <1,即
<1,即 <|y1-y2|
<|y1-y2| ,可得r=
,可得r= |y1-y2|∈(
|y1-y2|∈( ,
, )
)
∴△NPQ内切圆的半径的取值范围为( ,
, ).
).
点评:本题给出动点轨迹,求轨迹的方程并讨论截得三角形内切圆半径的取值范围.着重考查了点到直线的距离公式、垂直定理、一元二次方程根与系数的关系和函数单调性等知识,属于难题.
 +y2=1;再由圆的定义即可得到动点G的轨迹C2的方程为x2+y2=4;
+y2=1;再由圆的定义即可得到动点G的轨迹C2的方程为x2+y2=4;(II)由题意得直线l与x轴不垂直,设l方程为y=k(x+1),利用点到直线的距离公式结合垂径定理,算出|AB|=2
 .设P(x1,y1)、Q(x2,y2),△NPQ内切圆半径r满足
.设P(x1,y1)、Q(x2,y2),△NPQ内切圆半径r满足 |NF|•|y1-y2|=
|NF|•|y1-y2|= •r•(|PN|+|PQ|+|QN|),结合题中数据得到r=
•r•(|PN|+|PQ|+|QN|),结合题中数据得到r= |y1-y2|,由直线方程与椭圆消去x,得关于y的二次方程,再利用根与系数的关系算出|y1-y2|关于k的式子,从而得到r关于k的函数关系式,结合函数的单调性讨论可得r的取值范围.
|y1-y2|,由直线方程与椭圆消去x,得关于y的二次方程,再利用根与系数的关系算出|y1-y2|关于k的式子,从而得到r关于k的函数关系式,结合函数的单调性讨论可得r的取值范围.解答:解:(I)∵四边形MNEF是平行四边形,周长为4

∴点E到点F、N的距离之和等于2
 (定长),且|NF|=2<2
(定长),且|NF|=2<2
由椭圆的定义,得曲线C1的方程为
 +
+ =1(a>b>0)
=1(a>b>0)可得a=
 ,c=1,b2=a2-c2=1,
,c=1,b2=a2-c2=1,∴曲线C1的方程为
 +y2=1
+y2=1∵|
 |=2,∴动点G的轨迹为以原点为圆心,半径为2的圆
|=2,∴动点G的轨迹为以原点为圆心,半径为2的圆即曲线C2的方程为x2+y2=4;
(II)当l垂直x轴时,令x=-1代入曲线C2的方程得y=

∴|AB|=2
 ∉(
∉( ),不符合题意
),不符合题意因此直线l与x轴不垂直,设l方程为y=k(x+1)
原点到直线l的距离为d=
 ,
,由圆的几何性质,得到|AB|=2
 =2
=2 =2
=2
由|AB|∈(
 ),解之得k2>
),解之得k2>
联解
 ,消去x得(2+
,消去x得(2+ )y2-
)y2- y-1=0
y-1=0设P(x1,y1),Q(x2,y2),△NPQ内切圆的半径为r
可得y1+y2=
 =
= ,y1y2=-
,y1y2=- =-
=-
∵
 |NF|•|y1-y2|=
|NF|•|y1-y2|= •r•(|PN|+|PQ|+|QN|),其中|NF|=2,|PN|+|PQ|+|QN|=4
•r•(|PN|+|PQ|+|QN|),其中|NF|=2,|PN|+|PQ|+|QN|=4
∴r=
 |y1-y2|
|y1-y2|而|y1-y2|=
 =
= =
=
∵
 ,∴1-
,∴1-

别处,因为1-
 <1,即
<1,即 <|y1-y2|
<|y1-y2| ,可得r=
,可得r= |y1-y2|∈(
|y1-y2|∈( ,
, )
)∴△NPQ内切圆的半径的取值范围为(
 ,
, ).
).点评:本题给出动点轨迹,求轨迹的方程并讨论截得三角形内切圆半径的取值范围.着重考查了点到直线的距离公式、垂直定理、一元二次方程根与系数的关系和函数单调性等知识,属于难题.

练习册系列答案
相关题目
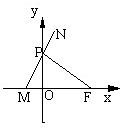 如图,已知定点F(1,0),动点P在y轴上运动,过点P作PM⊥PF并交x轴于M点,延长MP到N,使|PN|=|PM|.
如图,已知定点F(1,0),动点P在y轴上运动,过点P作PM⊥PF并交x轴于M点,延长MP到N,使|PN|=|PM|. (2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4
(2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4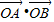 =-4,且
=-4,且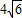 ≤|AB|≤
≤|AB|≤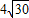 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
 =-4,且
=-4,且 ≤|AB|≤
≤|AB|≤ ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
 =-4,且
=-4,且 ≤|AB|≤
≤|AB|≤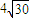 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.