题目内容
已知在等差数列{an}中，a1=31，Sn是它的前n项的和，S10=S22。
（1）求Sn；
（2）这个数列的前多少项的和最大，并求出这个最大值。
（1）求Sn；
（2）这个数列的前多少项的和最大，并求出这个最大值。
解：（1）∵S10=a1+a2+····+a10，S22= a1+a2+····+a22，
又S10= S22，
∴a11+a12+····+a22=0，
即a11+a22=2a1+31d=0，
又a1=31，
∴d=-2，
∴
。
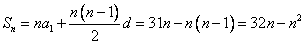（2）由（1）知，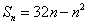
，
∴当n=16时，Sn有最大值，Sn的最大值是256。
又S10= S22，
∴a11+a12+····+a22=0，
即a11+a22=2a1+31d=0，
又a1=31，
∴d=-2，
∴
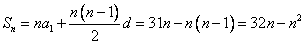。（2）由（1）知，
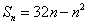，∴当n=16时，Sn有最大值，Sn的最大值是256。
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
已知在等差数列{an}中，a1=120，d=-4，若Sn≤an（n≥2），则n的最小值为（ ）
| A、60 | B、62 | C、70 | D、72 |
已知在等差数列{an}中3a2=7a7，a1＞0，则下列说法正确的是（ ）
| A、a11＞0 | B、S10为Sn的最大值 | C、d＞0 | D、S4＞S16 |