题目内容
平面内与两定点 、
、
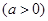 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上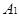 、
、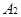 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与 值的关系。
值的关系。
【解析】本试题主要考查了平面中动点的轨迹方程,利用斜率之积为定值可以对参数进行分类讨论,并得到关于不同曲线的参数的范围问题。对于方程的特点做了很好的考查和运用。
【答案】
解:设动点为 ,其坐标为
,其坐标为 ,
,
当 时,由条件可得
时,由条件可得 ,即
,即 .又
.又 、
、 的坐标满足
的坐标满足 ,
,
故依题意,曲线 的方程为
的方程为 .
.
当 时,曲线
时,曲线 的方程为
的方程为 ,
, 是焦点在
是焦点在 轴上的椭圆;
轴上的椭圆;
当 时,曲线
时,曲线 的方程为
的方程为 ,
, 是圆点在原点的圆;
是圆点在原点的圆;
当 时,曲线
时,曲线 的方程为
的方程为 ,
, 是焦点在
是焦点在 轴上的椭圆;
轴上的椭圆;
当 时,曲线
时,曲线 的方程为
的方程为 ,
, 是焦点在
是焦点在 轴上的双曲线.
轴上的双曲线.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 、
、
 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上 、
、 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线