题目内容
函数f(x)=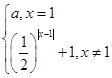 ,若关于x的方程2[f(x)]2-(2a+3)·f(x)+3a=0有五个不同的实数解,求a的取值范围.
,若关于x的方程2[f(x)]2-(2a+3)·f(x)+3a=0有五个不同的实数解,求a的取值范围.
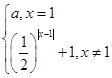 ,若关于x的方程2[f(x)]2-(2a+3)·f(x)+3a=0有五个不同的实数解,求a的取值范围.
,若关于x的方程2[f(x)]2-(2a+3)·f(x)+3a=0有五个不同的实数解,求a的取值范围. ∪
∪ .
.解:由2[f(x)]2-(2a+3)f(x)+3a=0得f(x)= 或f(x)=a.由已知画出函数f(x)的大致图像,要使关于x的方程2[f(x)]2-(2a+3)f(x)+3a=0有五个不同的实数解,即要使函数y=f(x)的图像与直线y=
或f(x)=a.由已知画出函数f(x)的大致图像,要使关于x的方程2[f(x)]2-(2a+3)f(x)+3a=0有五个不同的实数解,即要使函数y=f(x)的图像与直线y= 、y=a共有五个不同的交点,结合图像不难得出,a的取值范围是
、y=a共有五个不同的交点,结合图像不难得出,a的取值范围是 ∪
∪ .
.

 或f(x)=a.由已知画出函数f(x)的大致图像,要使关于x的方程2[f(x)]2-(2a+3)f(x)+3a=0有五个不同的实数解,即要使函数y=f(x)的图像与直线y=
或f(x)=a.由已知画出函数f(x)的大致图像,要使关于x的方程2[f(x)]2-(2a+3)f(x)+3a=0有五个不同的实数解,即要使函数y=f(x)的图像与直线y= 、y=a共有五个不同的交点,结合图像不难得出,a的取值范围是
、y=a共有五个不同的交点,结合图像不难得出,a的取值范围是 ∪
∪ .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
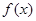 是二次函数,不等式
是二次函数,不等式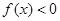 的解集是(0,5),且
的解集是(0,5),且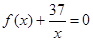 在区间
在区间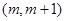 内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.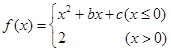 ,若
,若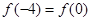 ,
,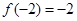 ,则关于
,则关于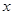 的方程
的方程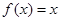 的解的个数为 ( )
的解的个数为 ( ) )x-sinx在区间[0,2π]上的零点个数为( )
)x-sinx在区间[0,2π]上的零点个数为( ) x=
x= 的解x0∈
的解x0∈ ,则正整数n=________.
,则正整数n=________. ,若关于
,若关于 的函数
的函数 有两个零点, 则实数
有两个零点, 则实数 的取值范围是__________.
的取值范围是__________.