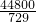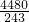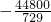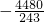题目内容
已知一非零的向量列
满足:
=(1,1),
=(xn,yn)=
(xn-1-yn-1,xn-1+yn-1)(n≥2).
(1)计算|
|,|
|,|
|;证明:数列{|
|}是等比数列;
(2)设θn(n≥2)是
,
的夹角的弧度数,bn=
,Sn=b2+b3+…+bn,求S2013.
| an |
| a1 |
| an |
| 1 |
| 2 |
(1)计算|
| a1 |
| a2 |
| a3 |
| an |
(2)设θn(n≥2)是
| an-1 |
| an |
| π |
| 4n(n-1)θn |
(1)∵非零向量列{
}满足:
=(1,1),
=(xn,yn)=
(xn-1-yn-1,xn-1+yn-1) (n≥2),
∴
=(1,1),
=
(0,2)=(0,1),
=
(-1,1)=(-
,
),
∴|
|=
=
,|
|=
=1,|
|=
=
.
∵|
|=
,
∴|
|=
=
=
,
∴
=
(常数),
∴{|
|}是首项|
|=
,公比q=
的等比数列.
(2)∵
•
=(xn-1,yn-1)•
(xn-1-yn-1,xn-1+yn-1)
=
(xn-12+yn-12)=
|
|2,
∴cosθn=
=
=
,
∴θn=
,n≥2.
∴bn=
=
=
=
-
,
∴Sn=b2+b3+…+bn
=(1-
)+(
-
)+…+(
-
)
=1-
.
∴S2013=1-
=
.
| an |
| a1 |
| an |
| 1 |
| 2 |
∴
| a1 |
| a2 |
| 1 |
| 2 |
| a3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴|
| a1 |
| 12+12 |
| 2 |
| a2 |
| 02+12 |
| a3 |
(-
|
| ||
| 2 |
∵|
| an |
| xn2+yn2 |
∴|
| an+1 |
| xn+12+yn+12 |
(
|
| ||
| 2 |
| xn2+yn2 |
∴
|
| ||
|
|
| ||
| 2 |
∴{|
| an |
| a1 |
| 2 |
| ||
| 2 |
(2)∵
| an-1 |
| an |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| an-1 |
∴cosθn=
| ||||
|
|
| ||||
|
|
| ||
| 2 |
∴θn=
| π |
| 4 |
∴bn=
| π |
| 4n(n-1)θn |
| π | ||
4n(n-1)•
|
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
∴Sn=b2+b3+…+bn
=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
=1-
| 1 |
| n |
∴S2013=1-
| 1 |
| 2013 |
| 2012 |
| 2013 |

练习册系列答案
相关题目
定义:如果一个向量列从第二项起,每一项与它的前一项的差都等于同一个常向量,那么这个向量列叫做等差向量列,这个常向量叫做等差向量列的公差.已知向量列{
}是以
=(1,3)为首项,公差
=(1,0)的等差向量列.若向量
与非零向量
=(xn,xn+1)(n∈N*)垂直,则
=( )
| an |
| a1 |
| d |
| an |
| bn |
| x10 |
| x1 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
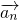 是以
是以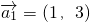 为首项,公差
为首项,公差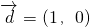 的等差向量列.若向量
的等差向量列.若向量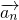 与非零向量
与非零向量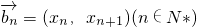 垂直,则
垂直,则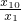 =
=