题目内容
已知α,β∈(0,π),sinα= ,sin(α+β)=
,sin(α+β)= ,则cosβ=________.
,则cosβ=________.
- ,或
,或
分析:①当α为锐角时,则α+β为钝角,此时,求出cosα 和cos(α+β)的值,利用两角差的余弦公式求得cosβ=cos[(α+β)-α]的值.②当α为钝角时,则α+β为钝角,此时,求出cosα 和cos(α+β) 的值,再利用两角差的余弦公式求得cosβ=cos[(α+β)-α]的值.
解答:∵已知α,β∈(0,π),sinα= ,sin(α+β)=
,sin(α+β)= ,sinα>sin(α+β),
,sinα>sin(α+β),
∴①当α为锐角时,则α+β为钝角,此时,cosα= ,cos(α+β)=-
,cos(α+β)=- ,
,
cosβ=cos[(α+β)-α]=cos(α+β) cosα+sin(α+β) sinα=- ×
× +
+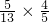 =-
=- .
.
②当α为钝角时,则α+β为钝角,此时,cosα=- ,cos(α+β)=-
,cos(α+β)=- ,
,
cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=- ×(-
×(- )+
)+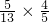 =
= ,
,
故答案为- ,或
,或 .
.
点评:本题主要考查两角和差的余弦公式的应用,同角三角函数的基本关系,体现了分类讨论的数学思想,属于中档题.
 ,或
,或
分析:①当α为锐角时,则α+β为钝角,此时,求出cosα 和cos(α+β)的值,利用两角差的余弦公式求得cosβ=cos[(α+β)-α]的值.②当α为钝角时,则α+β为钝角,此时,求出cosα 和cos(α+β) 的值,再利用两角差的余弦公式求得cosβ=cos[(α+β)-α]的值.
解答:∵已知α,β∈(0,π),sinα=
 ,sin(α+β)=
,sin(α+β)= ,sinα>sin(α+β),
,sinα>sin(α+β),∴①当α为锐角时,则α+β为钝角,此时,cosα=
 ,cos(α+β)=-
,cos(α+β)=- ,
,cosβ=cos[(α+β)-α]=cos(α+β) cosα+sin(α+β) sinα=-
 ×
× +
+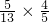 =-
=- .
.②当α为钝角时,则α+β为钝角,此时,cosα=-
 ,cos(α+β)=-
,cos(α+β)=- ,
,cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-
 ×(-
×(- )+
)+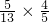 =
= ,
,故答案为-
 ,或
,或 .
.点评:本题主要考查两角和差的余弦公式的应用,同角三角函数的基本关系,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 如图所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程.
如图所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程.