题目内容
直三棱柱ABC-A1B1C1的底面是边长为3的正三角形,且侧棱长为2,则这个三棱柱的外接球的体积为
- A.

- B.4π
- C.
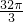
- D.16π
C
分析:先根据题意画出图形,再设三棱柱外接球的球半径为r,利用在直角三角形ADO中的边的关系求出球半径,最后利用球的体积公式即可求出这个三棱柱的外接球的体积.
解答: 解:设三棱柱外接球的球心为O,球半径为r,
解:设三棱柱外接球的球心为O,球半径为r,
三棱柱的底面三角形ABC的中心为D,如图,
有:OA=r,由于三棱柱的高为2,∴OD=1,
又在正三角形ABC中,AB=3,则AD= ,
,
∴在直角三角形ADO中,OA2=OD2+AD2有r2=12+( )2,
)2,
∴r=2,
则这个三棱柱的外接球的体积为V= ×r3=
×r3=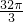 .
.
故选C.
点评:本题是基础题,考查几何体的外接球的体积的应用,三棱柱的性质等,考查计算能力.
分析:先根据题意画出图形,再设三棱柱外接球的球半径为r,利用在直角三角形ADO中的边的关系求出球半径,最后利用球的体积公式即可求出这个三棱柱的外接球的体积.
解答:
 解:设三棱柱外接球的球心为O,球半径为r,
解:设三棱柱外接球的球心为O,球半径为r,三棱柱的底面三角形ABC的中心为D,如图,
有:OA=r,由于三棱柱的高为2,∴OD=1,
又在正三角形ABC中,AB=3,则AD=
 ,
,∴在直角三角形ADO中,OA2=OD2+AD2有r2=12+(
 )2,
)2,∴r=2,
则这个三棱柱的外接球的体积为V=
 ×r3=
×r3=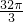 .
.故选C.
点评:本题是基础题,考查几何体的外接球的体积的应用,三棱柱的性质等,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB1=
直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB1= 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角. 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( )
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( ) 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是







