题目内容
12.已知函数f(x)=$\frac{x-1}{lnx}$.(Ⅰ)试判断函数y=f(x)在(1,+∞)上的单调性;
(Ⅱ)令an+1=f(an)(n∈N•),若a1=$\sqrt{e}$,求证2nlnan≥1.
分析 (Ⅰ)先求出函数f(x)的导数,令g(x)=xlnx-x+1,通过求导得到g(x)在(1,+∞)单调递增,从而求出f(x)的单调性;
(Ⅱ)用数学归纳法证明:(1)n=1时,命题成立,(2)假设n=k时,命题成立,再证出n=k+1时命题成立即可.
解答 解:(Ⅰ)∵f′(x)=$\frac{xlnx-x+1}{{x(lnx)}^{2}}$,
当x∈(1,+∞)时,有x(lnx)2>0,
故只需考察函数g(x)=xlnx-x+1在(1,+∞)的函数值变化,
而g′(x)=lnx+1-1=lnx,
当x∈(1,+∞)时,g′(x)=lnx>0,
故g(x)在(1,+∞)单调递增,
则有:g(x)>g(1)=0,
∴x∈(1,+∞)时,f′(x)>0,
∴y=f(x)在(1,+∞)单调递增;
(Ⅱ)下面用数学归纳法证明:
(1)当n=1时,a1=$\sqrt{e}$,∴2lna1=2ln$\sqrt{e}$=1,
∴n=1时,命题成立;
(2)假设n=k(k≥1)时,命题成立,即:2klnak≥1,
要证明n=k+1时,命题成立,即证明2k+1lnak+1≥1,只需证明ak+1≥${e}^{\frac{1}{{2}^{(k+1)}}}$,
依题意知ak+1=f(a1),即证明:f(a1)≥${e}^{\frac{1}{{2}^{(k+1)}}}$,
由归纳假设2klnak≥1,得ak≥${e}^{\frac{1}{{2}^{k}}}$>1,
由(Ⅰ)知:f(ak)≥f(${e}^{\frac{1}{{2}^{k}}}$)=$\frac{{e}^{\frac{1}{{2}^{k}}-1}}{\frac{1}{{2}^{k}}}$
若f(${e}^{\frac{1}{{2}^{k}}}$)≥${e}^{\frac{1}{{2}^{(k+1)}}}$,则必有f(ak)≥${e}^{\frac{1}{{2}^{(k+1)}}}$,
下面证明:f(${e}^{\frac{1}{{2}^{k}}}$)=$\frac{{e}^{\frac{1}{{2}^{k}}-1}}{\frac{1}{{2}^{k}}}$≥${e}^{\frac{1}{{2}^{(k+1)}}}$,
构造函数g(x)=ex-1-x${e}^{\frac{x}{2}}$(x>0),
则g′(x)=ex-${e}^{\frac{x}{2}}$-$\frac{x}{2}$${e}^{\frac{x}{2}}$=${e}^{\frac{x}{2}}$(${e}^{\frac{x}{2}}$-$\frac{x}{2}$),
∵x>0,∴${e}^{\frac{x}{2}}$>1,
由(Ⅰ)得:${e}^{\frac{x}{2}}$-1-$\frac{x}{2}$>0,
∴x>0时,g′(x)>0,则g(x)在(0,+∞)上递增,
则g($\frac{1}{{2}^{k}}$)>g(0),即:${e}^{\frac{1}{{2}^{k}}}$-1-$\frac{1}{{2}^{k}}$${e}^{\frac{1}{2}•\frac{1}{{2}^{k}}}$>0,
则:f(${e}^{\frac{1}{{2}^{k}}}$)=$\frac{{e}^{\frac{1}{{2}^{k}}-1}}{\frac{1}{{2}^{k}}}$>${e}^{\frac{1}{2}•\frac{1}{{2}^{k}}}$=${e}^{\frac{1}{2(k+1)}}$②,
由①②及题意得f(ak)≥${e}^{\frac{1}{{2}^{(k+1)}}}$,即2(k+1)lnak+1≥1,
综合(1)(2)得:对?n∈N•,都有2nlnan≥1成立.
点评 本题考察了函数的单调性,考察导数的应用,考察数学归纳法的应用,是一道难题.

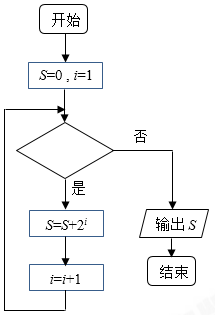
| A. | i≤4? | B. | i≤5? | C. | i≤6? | D. | i≤7? |
| A. | 720种 | B. | 600种 | C. | 360种 | D. | 300种 |
| A. | 10 | B. | 20 | C. | 4 | D. | 12 |
| A. | $\frac{1}{{{{({a_1}•{a_n})}^n}}}$ | B. | $\frac{1}{{{{({a_1}•{a_{n+1}})}^n}}}$ | C. | $\frac{1}{{{{({a_1}•{a_n})}^{n+1}}}}$ | D. | $\frac{1}{{{{({a_1}•{a_{n+1}})}^{n+1}}}}$ |