题目内容
已知函数f(x)=lnx①当0<a<b时,求证:
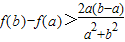
②设点P(0,1),求点P到f(x)图象上点的最近距离.
【答案】分析:①(a)-f(b)=lnb-lna=ln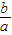 =-ln
=-ln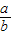 =-ln(1+
=-ln(1+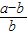 ),由(1)知ln(1+x)≤x,f(b)-f(a)≥-
),由(1)知ln(1+x)≤x,f(b)-f(a)≥-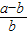 =
=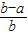 ,利用基本不等式即可证得结论.
,利用基本不等式即可证得结论.
②求出函数f(x)=lnx的反函数为f-1(x)=ex,根据互为反函数的图象关于直线y=x对称,由f(x)在(1,0)点的导数为1,f-1(x)在(0,1)点的导数为1,均与对称轴的斜率相等,可得故(1,0)点和(0,1)点是函数f(x)与函数f-1(x)的图象上所有对称点中距离最近的一组,进而求出点P到f(x)图象上点的最近距离
解答:证明:①f(a)-f(b)=lnb-lna=ln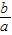 =-ln
=-ln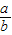 =-ln(1+
=-ln(1+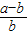 )
)
由(1)知ln(1+x)≤x,f(b)-f(a)≥-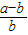 =
=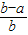
又∵0<a<b,
∴a2+b2>2ab,
∴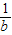 >
>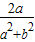
∴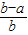 >
>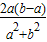
∴f(b)-f(a)>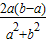
解:②函数f(x)=lnx的反函数为f-1(x)=ex其图象过(0,1)点
且函数f(x)与函数f-1(x)的图象关于直线y=x对称
由f(x)在(1,0)点的导数为1,f-1(x)在(0,1)点的导数为1,均与对称轴的斜率相等
故(1,0)点和(0,1)点是函数f(x)与函数f-1(x)的图象上所有对称点中距离最近的一组
故点P到f(x)图象上点的最近距离,即为(1,0)点和(0,1)点的距离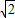
点评:本题考查导数知识的运用,考查函数的最值,考查不等式的证明,正确运用结论是关键.
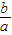 =-ln
=-ln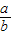 =-ln(1+
=-ln(1+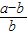 ),由(1)知ln(1+x)≤x,f(b)-f(a)≥-
),由(1)知ln(1+x)≤x,f(b)-f(a)≥-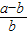 =
=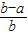 ,利用基本不等式即可证得结论.
,利用基本不等式即可证得结论.②求出函数f(x)=lnx的反函数为f-1(x)=ex,根据互为反函数的图象关于直线y=x对称,由f(x)在(1,0)点的导数为1,f-1(x)在(0,1)点的导数为1,均与对称轴的斜率相等,可得故(1,0)点和(0,1)点是函数f(x)与函数f-1(x)的图象上所有对称点中距离最近的一组,进而求出点P到f(x)图象上点的最近距离
解答:证明:①f(a)-f(b)=lnb-lna=ln
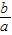 =-ln
=-ln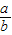 =-ln(1+
=-ln(1+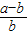 )
)由(1)知ln(1+x)≤x,f(b)-f(a)≥-
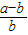 =
=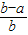
又∵0<a<b,
∴a2+b2>2ab,
∴
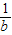 >
>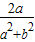
∴
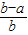 >
>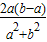
∴f(b)-f(a)>
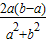
解:②函数f(x)=lnx的反函数为f-1(x)=ex其图象过(0,1)点
且函数f(x)与函数f-1(x)的图象关于直线y=x对称
由f(x)在(1,0)点的导数为1,f-1(x)在(0,1)点的导数为1,均与对称轴的斜率相等
故(1,0)点和(0,1)点是函数f(x)与函数f-1(x)的图象上所有对称点中距离最近的一组
故点P到f(x)图象上点的最近距离,即为(1,0)点和(0,1)点的距离
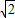
点评:本题考查导数知识的运用,考查函数的最值,考查不等式的证明,正确运用结论是关键.

练习册系列答案
相关题目