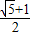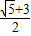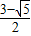题目内容
已知双曲线M: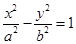 和双曲线:
和双曲线: ,其中b>a>0,且双曲线M与N的交点在两坐标轴上的射影恰好是两双曲线的焦点,则双曲线M的离心率为( )
,其中b>a>0,且双曲线M与N的交点在两坐标轴上的射影恰好是两双曲线的焦点,则双曲线M的离心率为( )
A、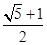 B、
B、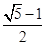 C、
C、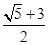 D、
D、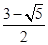
【答案】
A
【解析】解:∵双曲线M方程为: ,双曲线N方程为:
,双曲线N方程为: 其中b>a>0,
其中b>a>0,
∴两个双曲线的焦距相等,设为个焦距为2c,其中c满足:c2= a2+b2∵双曲线M与N的交点在两坐标轴上的射影恰好是两双曲线的焦点,
∴交点坐标为:(c,c),代入双曲线M(或双曲线N)的方程,得
c2 /a2 -c2 /b2 =1,结合b2=c2-a2得:c2/ a2 -c2 /c2-a2 =1,
去分母,得c2(c2-a2)-a2c2=a2(c2-a2),
整理,得c4-3a2c4+a4=0,所以e4-3e2+1=0,解之得e2= =(
=(
 )2(另一值小于1舍去)
)2(另一值小于1舍去)
∴双曲线M的离心率e= 

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
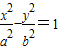 和双曲线N:
和双曲线N: ,其中b>a>0,且双曲线M与N的交点在两坐标轴上的射影恰好是两双曲线的焦点,则双曲线M的离心率为( )
,其中b>a>0,且双曲线M与N的交点在两坐标轴上的射影恰好是两双曲线的焦点,则双曲线M的离心率为( )