题目内容
已知函数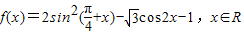 ,若函数h(x)=f(x+α)的图象关于点
,若函数h(x)=f(x+α)的图象关于点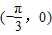 对称,且α∈(0,π),则α=( )
对称,且α∈(0,π),则α=( )A.
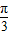
B.
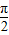
C.
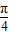
D.
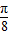
【答案】分析:利用二倍角公式可求得f(x)=2sin(2x-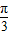 ),从而知h(x)=f(x+α)=2sin(2x+2α-
),从而知h(x)=f(x+α)=2sin(2x+2α-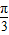 ),利用其图象关于(-
),利用其图象关于(-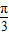 ,0)对称即可求得α.
,0)对称即可求得α.
解答:解:∵f(x)=1-cos(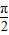 +2x)-
+2x)-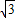 cos2x-1
cos2x-1
=sin2x-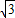 cos2x
cos2x
=2sin(2x-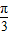 ),
),
∴h(x)=f(x+α)=2sin(2x+2α-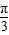 ),
),
∵其图象关于(-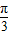 ,0)对称,
,0)对称,
∴2×(-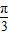 )+2α-
)+2α-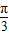 =kπ,k∈Z,
=kπ,k∈Z,
∴2α=(k+1)π,k∈Z.
∴α=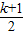 π,又α∈(0,π),
π,又α∈(0,π),
∴α=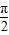 .
.
故选B.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,着重考查正弦函数的对称性,属于中档题.
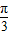 ),从而知h(x)=f(x+α)=2sin(2x+2α-
),从而知h(x)=f(x+α)=2sin(2x+2α-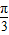 ),利用其图象关于(-
),利用其图象关于(-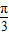 ,0)对称即可求得α.
,0)对称即可求得α.解答:解:∵f(x)=1-cos(
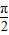 +2x)-
+2x)-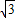 cos2x-1
cos2x-1=sin2x-
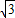 cos2x
cos2x=2sin(2x-
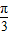 ),
),∴h(x)=f(x+α)=2sin(2x+2α-
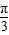 ),
),∵其图象关于(-
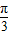 ,0)对称,
,0)对称,∴2×(-
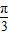 )+2α-
)+2α-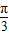 =kπ,k∈Z,
=kπ,k∈Z,∴2α=(k+1)π,k∈Z.
∴α=
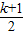 π,又α∈(0,π),
π,又α∈(0,π),∴α=
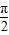 .
.故选B.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,着重考查正弦函数的对称性,属于中档题.

练习册系列答案
相关题目
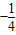 ,在x=-2处的切线与直线x-8y=0垂直.
,在x=-2处的切线与直线x-8y=0垂直.