题目内容

已知函数f（x）=2ax+1-3a在（0，1）内存在一个零点，则实数a的取值范围是

A.
$数学公式$
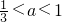
B.
$数学公式$
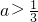
C.
a＞1或 $数学公式$
D.
a＜1

A
分析：由题意可得，f（0）f（1）=（1-3a）（1-a）＜0，解不等式求得实数a的取值范围．
解答：已知函数f（x）=2ax+1-3a在（0，1）内存在一个零点，故有 f（0）f（1）=（1-3a）（1-a）＜0，
解得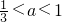 $\text{[math]}$ ，
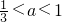故选A．
点评：本题主要考查函数的零点的判定定理的应用，一元二次不等式的解法，属于基础题．

练习册系列答案

0系列答案

仁爱英语教材讲解系列答案

仁爱英语暑假补课专用教材系列答案

仁爱英语英汉互动讲解系列答案

仁爱英语同步阅读与完形填空周周练系列答案

拔尖特训系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

已知函数f（x）=2-

，（x＞0），若存在实数a，b（a＜b），使y=f（x）的定义域为（a，b）时，值域为（ma，mb），则实数m的取值范围是（　　）

A．（-∞，1）

B．（0，1）

D．（-1，1）

已知函数f（x）=2+log_0.5x（x＞1），则f（x）的反函数是（　　）

A．f^-1（x）=2^2-x（x＜2）

B．f^-1（x）=2^2-x（x＞2）

C．f^-1（x）=2^x-2（x＜2）

D．f^-1（x）=2^x-2（x＞2）

已知函数f（x）=2（m-1）x²-4mx+2m-1
（1）m为何值时，函数的图象与x轴有两个不同的交点；
（2）如果函数的一个零点在原点，求m的值．

（2013•上海）已知函数f（x）=2-|x|，无穷数列{a_n}满足a_n+1=f（a_n），n∈N^*
（1）若a₁=0，求a₂，a₃，a₄；
（2）若a₁＞0，且a₁，a₂，a₃成等比数列，求a₁的值
（3）是否存在a₁，使得a₁，a₂，…，a_n，…成等差数列？若存在，求出所有这样的a₁，若不存在，说明理由．

选修4-5：不等式选讲
已知函数f（x）=2|x-2|-x+5，若函数f（x）的最小值为m
（Ⅰ）求实数m的值；
（Ⅱ）若不等式|x-a|+|x+2|≥m恒成立，求实数a的取值范围．