题目内容
己知椭圆 的离心率为
的离心率为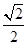 ,
,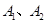 是椭圆的左右顶点,
是椭圆的左右顶点,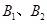 是椭圆的上下顶点,四边形
是椭圆的上下顶点,四边形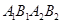 的面积为
的面积为 .
.
(1)求椭圆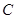 的方程;
的方程;
(2)圆 过
过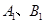 两点.当圆心
两点.当圆心 与原点
与原点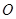 的距离最小时,求圆
的距离最小时,求圆 的方程.
的方程.
(1)  (2)
(2) 
解析试题分析:解:(1)依题意有: ① 2分
① 2分
四边形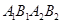 是以椭圆
是以椭圆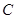 的四顶点为顶点的菱形
的四顶点为顶点的菱形
可得: 即
即 ② 4分
② 4分
由①、②解得: 所以椭圆
所以椭圆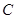 的方程为:
的方程为: 6分
6分
(2)依题意得
可得 的垂直平分线
的垂直平分线 的方程为:
的方程为: ③ 8分
③ 8分
圆心 在
在 上,当圆心
上,当圆心 与原点
与原点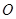 的距离最小时,
的距离最小时,
可得 的方程为
的方程为 ④ 10分
④ 10分
联立③、④得 ,即
,即 12分
12分
由此可得 ,
,
所以圆 的方程为:
的方程为: 14分
14分
考点:椭圆方程,圆的方程
点评:解决的关键是利用椭圆的几何性质来得到其方程,同时能借助于直线与圆的关系来得到圆的方程,属于基础题。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 的焦点为
的焦点为 ,过焦点
,过焦点 轴的动直线
轴的动直线 交抛物线于
交抛物线于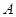 ,
, 两点,抛物线在
两点,抛物线在 .
.
 交该抛物线于
交该抛物线于 ,
,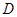 两点,求四边形
两点,求四边形 面积的最小值.
面积的最小值.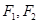 是椭圆的左、右焦点,O为坐标原点,点P
是椭圆的左、右焦点,O为坐标原点,点P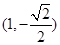 在椭圆上,线段
在椭圆上,线段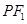 与y轴的交点M满足
与y轴的交点M满足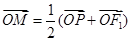
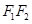 为直径的圆,直线
为直径的圆,直线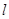 :
: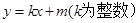 与圆相切,并与椭圆交于不同的两点
与圆相切,并与椭圆交于不同的两点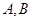 ,当
,当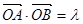 ,且满足
,且满足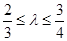 时,求直线
时,求直线 到点
到点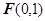 的距离与点
的距离与点 轴的距离的差等于1.(I)求动点
轴的距离的差等于1.(I)求动点 的方程;(II)过点
的方程;(II)过点 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线 ,设
,设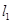 与轨迹
与轨迹 ,
,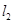 与轨迹
与轨迹 ,求
,求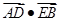 的最小值.
的最小值.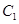 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为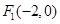 ,
,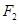
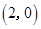 ,点
,点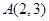 在椭圆
在椭圆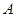 的直线
的直线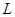 与抛物线
与抛物线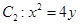 交于
交于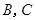 两点,抛物线
两点,抛物线 在点
在点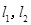 ,且
,且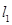 与
与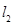 交于点
交于点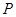 .
. 的点
的点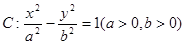 的两个焦点为
的两个焦点为 的曲线C上.(Ⅰ)求双曲线C的方程;
的曲线C上.(Ⅰ)求双曲线C的方程;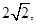 求直线l的方程
求直线l的方程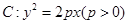 的焦点为
的焦点为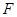 ,经过点
,经过点 交抛物线
交抛物线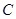 于点
于点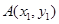 ,
,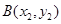 且
且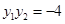 .
.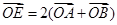 (
( 为坐标原点),且点
为坐标原点),且点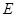 在抛物线
在抛物线 是抛物线
是抛物线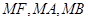 的斜率分别为
的斜率分别为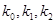 .求证:
.求证: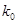 为定值时,
为定值时,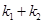 也为定值.
也为定值. 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为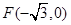 ,右顶点为
,右顶点为 ,设点
,设点 .
. 是椭圆上的动点,求线段
是椭圆上的动点,求线段 中点
中点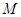 的轨迹方程;
的轨迹方程; 的直线交椭圆于点
的直线交椭圆于点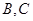 ,求
,求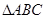 面积的最大值。
面积的最大值。 的中心在原点,焦点在
的中心在原点,焦点在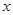 轴上,一条经过点
轴上,一条经过点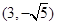 且方向向量为
且方向向量为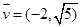 的直线
的直线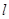 交椭圆
交椭圆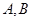 两点,交
两点,交 点,且
点,且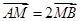 .
.