Question

数列{a_n}的前n项和为S_n．已知．

（Ⅰ）若a₁=1，求a₂，a₃，a₄；

（Ⅱ）若a₁=a（a为常数），求数列{a_n}的通项公式；

（Ⅲ）设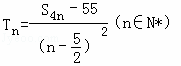，求数列{T_n}的最大项．

Answer 1

考点：

数列递推式；数列的函数特性．

专题：

等差数列与等比数列．

分析：

（Ⅰ）直接利用数列的递推公式，分别令n=1，2，3依次计算可求得a₂，a₃，a₄；

（Ⅱ）在中，分别以2n，2n﹣1代n（第Ⅰ问已做了由特殊到一般的铺垫），得出 a_2n+1+a_2n=4n﹣1，a_2n﹣a_2n﹣1=4n﹣3．继而得出 a₃=2﹣a₁，a_2n+3+a_2n+1=2，所以 a_2n+3=a_2n﹣1（n∈N*）．当n=2k（k∈N*）时，a_4k+3=a_4k﹣1=…=a₃=2﹣a₁；当n=2k﹣1（k∈N*）时，a_4k+1=a_4k﹣3=…=a₁．由已知可得a_4k﹣1+a_4k﹣2=8k﹣5，a_4k﹣a_4k﹣1=8k﹣3（k∈N^*）．所以 a_4k﹣2=8k﹣5﹣a_4k﹣1=8k﹣7+a₁，a_4k=8k﹣3+a_4k﹣1=8k﹣1﹣a₁．最后得出分段形式的通项公式．

（Ⅲ）在求出（Ⅱ）的基础上，应用分组求和法，得出 ．继而 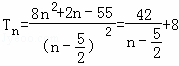．再利用函数的思想研究其单调性，求出数列{T_n}的最大项．

解答：

（本小题满分11分）

解：（Ⅰ）因为 ，a₁=1，

所以当n=1时，有a₂﹣a₁=1，得出 a₂=2，

同理当n=2时求得a₃=1，

当n=3时求得a₄=6．…（2分）

（Ⅱ）因为 ，

所以 a_2n+1+a_2n=4n﹣1，a_2n﹣a_2n﹣1=4n﹣3．

两式相减得a_2n+1+a_2n﹣1=2．

所以 a₃=2﹣a₁，a_2n+3+a_2n+1=2，

所以 a_2n+3=a_2n﹣1（n∈N*）．

当n=2k（k∈N*）时，a_4k+3=a_4k﹣1=…=a₃=2﹣a₁；

当n=2k﹣1（k∈N*）时，a_4k+1=a_4k﹣3=…=a₁．

由已知可得a_4k﹣1+a_4k﹣2=8k﹣5，a_4k﹣a_4k﹣1=8k﹣3（k∈N*）．

所以 a_4k﹣2=8k﹣5﹣a_4k﹣1=8k﹣7+a₁，a_4k=8k﹣3+a_4k﹣1=8k﹣1﹣a₁．

因为 a₁=a，

所以 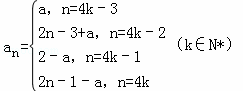．…（7分）

（Ⅲ）设b_n=a_4n﹣3+a_4n﹣2+a_4n﹣1+a_4n（n∈N*），则S_4n=b₁+b₂+…+b_n．

类似（Ⅱ）可得 b_n=a_4n﹣3+a_4n﹣2+a_4n﹣1+a_4n=16n﹣6．

所以 {b_n}为首项为10，公差为16的等差数列．

所以 ．

因为 ，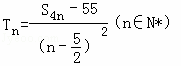

所以 ．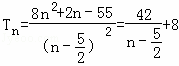

所以 T₁=﹣20，T₃=92．

因为 函数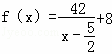的单调递减区间是，

所以 数列{T_n}的最大项是92．…（11分）

点评：

本题考查数列递推公式与通项公式的应用及求解，函数思想，分类与整合思想，以及由特殊到一般的认识问题解决问题的思维过程，考查逻辑思维能力，推理计算能力．