Question

【题目】已知函数f（x）在（0， ）上处处可导，若[f（x）﹣f′（x）]tanx﹣f（x）＜0，则（ ）
A.一定小于
B.一定大于
C.可能大于
D.可能等于

Answer 1

【答案】A
【解析】解：∵[f（x）﹣f′（x）]tanx﹣f（x）＜0，∴f（x）sinx＜f′（x）sinx+f（x）cosx．
令g（x）=f（x）sinx，则g′（x）=f′（x）sinx+f（x）cosx＞f（x）sinx=g（x）．∴g′（x）﹣g（x）＞0．
令h（x）= ，则h′（x）= ＞0．∴h（x）是增函数．
∴h（ln ）＜h（ln ），即 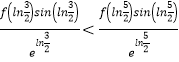，化简得f（ln ）sin（ln ）＜0.6f（ln ）sin（ln ）．
故选：A．
构造g（x）=f（x）sinx，根据已知条件判断g（x）与g′（x）的关系，再构造h（x）= ，判断h（x）的单调性，利用单调性得出结论．