题目内容
已知函数![]() ,且f(1)=
,且f(1)=![]() ,f(2)=
,f(2)=![]() .(1)求
.(1)求![]() ;(2)判断f(x)的奇偶性;(3)试判断函数在
;(2)判断f(x)的奇偶性;(3)试判断函数在![]() 上的单调性,并证明;
上的单调性,并证明;
![]() 20解:(1)由已知得:
20解:(1)由已知得:
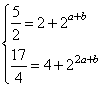 ,解得
,解得![]() .
.
(2)由上知![]() .任取
.任取![]() ,则
,则![]() ,所以
,所以![]() 为偶函数.
为偶函数.
(3)可知![]() 在
在![]() 上应为减函数.下面证明:
上应为减函数.下面证明:
任取![]() ,且
,且![]() ,则
,则
![]()
![]()
=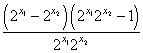 ,因为
,因为![]() ,且
,且![]() ,所以
,所以![]() ,从而
,从而
![]() ,
,![]() ,
,![]() , 故
, 故![]() ,由此得函数
,由此得函数![]() 在
在![]() 上为减函数
上为减函数

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
题目内容
已知函数![]() ,且f(1)=
,且f(1)=![]() ,f(2)=
,f(2)=![]() .(1)求
.(1)求![]() ;(2)判断f(x)的奇偶性;(3)试判断函数在
;(2)判断f(x)的奇偶性;(3)试判断函数在![]() 上的单调性,并证明;
上的单调性,并证明;
![]() 20解:(1)由已知得:
20解:(1)由已知得:
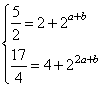 ,解得
,解得![]() .
.
(2)由上知![]() .任取
.任取![]() ,则
,则![]() ,所以
,所以![]() 为偶函数.
为偶函数.
(3)可知![]() 在
在![]() 上应为减函数.下面证明:
上应为减函数.下面证明:
任取![]() ,且
,且![]() ,则
,则
![]()
![]()
=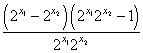 ,因为
,因为![]() ,且
,且![]() ,所以
,所以![]() ,从而
,从而
![]() ,
,![]() ,
,![]() , 故
, 故![]() ,由此得函数
,由此得函数![]() 在
在![]() 上为减函数
上为减函数

 通城学典默写能手系列答案
通城学典默写能手系列答案