题目内容
如图，港口B在港口O正东120海里处，小岛C在港口O北偏东60°方向，港口B北偏西30°方向上，一艘科学考察船从港口O出发，沿北偏东30°即OA方向以20海里/小时的速度驶离港口O，一艘快艇从港口B出发，以60海里/小时的速度驶向小岛C，在C岛装运补给物资后给考察船送去，现两船同时出发，补给物资的装船时间为1小时，问快艇离港口B后，最少要经过多少小时才能和考察船相遇？
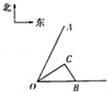
解：设快艇驶离港口B后，最少要经过x小时，在OA上的点D处与考察船相遇：如图， 连接CD，则快艇沿线段BC，CD航行，
在△OBC中，∠BOC=30°，∠CBD=60°
∴∠BCO=90°， 又BO=120，
∴BC=60，OC=60
，
故快艇从港口B到小岛C需要1小时，
在△OCD中，∠COD=30°，OD=20x，CD=60（x﹣2），
由余弦定理知CD2=OD2+OC2﹣2
OD
OCcos∠COD，
∴602（x﹣2）2=（20x）2+（60
）2﹣2
20x
60
cos30°，
解得x=3或x=
，
∵x＞1，∴x=3．
故快艇驶离港口B后，最少要经过3小时才能和考察船相遇．
在△OBC中，∠BOC=30°，∠CBD=60°
∴∠BCO=90°， 又BO=120，
∴BC=60，OC=60
，故快艇从港口B到小岛C需要1小时，
在△OCD中，∠COD=30°，OD=20x，CD=60（x﹣2），
由余弦定理知CD2=OD2+OC2﹣2
ODOCcos∠COD， ∴602（x﹣2）2=（20x）2+（60
）2﹣220x60cos30°，解得x=3或x=
，∵x＞1，∴x=3．
故快艇驶离港口B后，最少要经过3小时才能和考察船相遇．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，港口B在港口O正东120海里处，小岛C在港口O北偏东60°方向，港口B的北偏西30°方向上，一艘科学考察船从港口O出发，沿北偏东30°即OA方向以20海里/小时的速度驶离港口O，一艘快艇从港口B出发，以60海里/小时的速度驶向小岛C，在C岛装运补给物资后给考察船送去，现两船同时出发，补给物资的装船时间为1小时，问快艇离港口B后，最少要经过多少小时才能和考察船相遇？
