题目内容
已知函数 ,
, .
.
(Ⅰ)若 在
在 上为单调函数,求m的取值范围;
上为单调函数,求m的取值范围;
(Ⅱ)设 ,若在
,若在 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
(Ⅰ)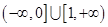 (Ⅱ)
(Ⅱ)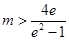
解析试题分析:(Ⅰ)f(x)-g(x)=mx-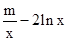 ,
,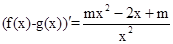
由于f(x)-g(x)在其定义域内为单调函数,则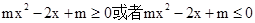 在
在 上恒成立,
上恒成立,
即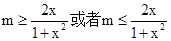 在
在 上恒成立,
上恒成立,
故 ,
,
综上,m的取值范围是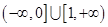 …6分
…6分
(Ⅱ)构造函数F(x)=f(x)-g(x)-h(x),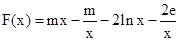 ,
,
当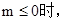 由
由 得,
得, ,
,
所以在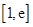 上不存在一个
上不存在一个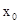 ,使得
,使得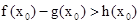 ; …………10分
; …………10分
当m>0时, ,
,
因为 ,所以
,所以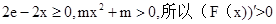 在
在 上恒成立,故F(x)在
上恒成立,故F(x)在 上单调递增,
上单调递增,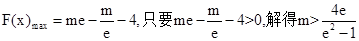 ,
,
故m的取值范围是 …………15分
…………15分
另法:(3) 令
令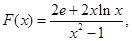
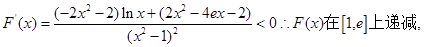
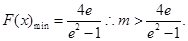
考点:利用函数导数判定单调性求函数最值
点评:若已知函数 在某区间上是增函数,则有
在某区间上是增函数,则有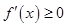 在该区间上恒成立;若已知函数
在该区间上恒成立;若已知函数 在某区间上是减函数,则有
在某区间上是减函数,则有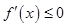 在该区间上恒成立。第二问首先将不等式成立转化为求函数最值,进而构造新函数,通过导数工具求其最值
在该区间上恒成立。第二问首先将不等式成立转化为求函数最值,进而构造新函数,通过导数工具求其最值

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 的定义域为
的定义域为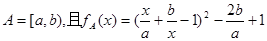 ,其中a、b为任
,其中a、b为任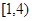 时,研究
时,研究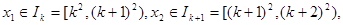 其中k是正整数,对一切正整数k不等式
其中k是正整数,对一切正整数k不等式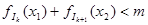 都有解,求m的取值范围。
都有解,求m的取值范围。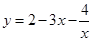 的值域.
的值域. ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 能作几条直线与曲线
能作几条直线与曲线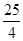 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.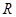 上的函数
上的函数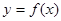 ,
,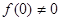 ,当
,当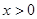 时,
时,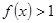 .且对任意的
.且对任意的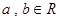 有
有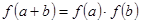 。
。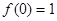 ;
;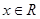 ,恒有
,恒有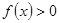 ;
;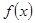 是
是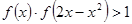 ,求
,求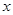 的取值范围。
的取值范围。 。
。 时,求函数
时,求函数 的最小值;
的最小值; 时,求实数
时,求实数 的取值范围。
的取值范围。 ,其图象在点
,其图象在点 处的切线方程为
处的切线方程为
 的值;
的值; 的单调区间,并求出
的单调区间,并求出