Question

已知函数f(x)=log₂,g(x)=log₂(x-2)+log₂(p-x),且p＞2,设F(x)=g(x)+f(x).

(1)求使f(x),g(x)同时有意义的x的取值范围；

(2)F(x)是否存在最大值或最小值？若存在，则求出它的最大值与最小值.

Answer 1

解:(1)由题意有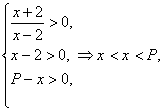

∴使f(x),g(x)同时有意义的x的取值范围是（2,p）.

(2)F(x)=log₂+log₂(x-2)+log₂(p-x)=log₂［(x+2)(p-x)］,x∈(2,p),

令y=log₂t,t=(x+2)(p-x)=-x²+(p-2)x+2p=-(x-)²+,

若≤2,即2＜p≤6时，t在（2,p）上单调递减.

因为F（x）的定义域是开区间，故f(x)此时无最大值也无最小值.

若≥p即p≤-2,此种情况不合题意，舍去.

若2＜＜p,即p＞6,则0＜t≤,

∴y≤log₂=2log₂(p+2)-2.

综上知，当2＜p≤6时，F(x)无最大值也无最小值；当p＞6时，F(x)的最大值为2log₂(p+2)-2，没有最小值.