题目内容
设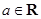 ,函数
,函数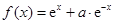 的导函数是
的导函数是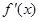 ,且
,且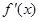 是奇函数.若曲线
是奇函数.若曲线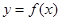 的一条切线的斜率是
的一条切线的斜率是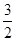 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.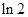 B.
B.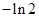 C.
C.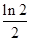 D.
D.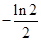
【答案】
A
【解析】
试题分析: ,因为
,因为 是奇函数,所以
是奇函数,所以 ,求得
,求得 ,则
,则
 。令所求切点为
。令所求切点为 ,则
,则 ,解得
,解得
 ,故
,故 。选A。
。选A。
考点:导数的应用
点评:导数经常用于求出曲线的切线,导数的几何意义就是切线的斜率。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数y=f(x)在(a,b)上的导函数为f′(x),f′(x)在(a,b)上的导函数为f″(x),若在a,b)上,f″(x)<0恒成立,则称函数函数f(x)在(a,b)上为“凸函数”.已知当m≤2时,f(x)=
x3-
mx2+x在(-1,2)上是“凸函数”.则f(x)在(-1,2)上( )
| 1 |
| 6 |
| 1 |
| 2 |
| A、既有极大值,也有极小值 |
| B、既有极大值,也有最小值 |
| C、有极大值,没有极小值 |
| D、没有极大值,也没有极小值 |
 ,函数
,函数 的导函数
的导函数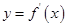 是奇函数,若曲线
是奇函数,若曲线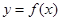 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标是( )
,则切点的横坐标是( ) B.
B.
 D.
D.
 ,函数
,函数 的导函数是
的导函数是 ,且
,且 的一条切线的斜率是
的一条切线的斜率是 ,则切点的横坐标为_______________.
,则切点的横坐标为_______________. ,函数
,函数 的导函数是
的导函数是 ,且
,且 的一条切线的斜率是
的一条切线的斜率是 ,则切点的横坐标为
( )
,则切点的横坐标为
( ) B.
B. C.
C. D.
D.