题目内容
设x1，x2是函数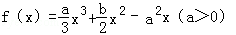
的两个极值点，且|x1﹣x2|=2．
（Ⅰ）证明：0＜a≤1；
（Ⅱ）证明：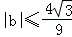
．
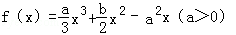的两个极值点，且|x1﹣x2|=2．（Ⅰ）证明：0＜a≤1；
（Ⅱ）证明：
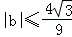．解：（Ⅰ）对f（x）求导可得f'（x）=ax2+bx﹣a2（a＞0）．
因为x1，x2是f（x）的两个极值点，
所以x1，x2是方程f'（x）=0的两个实根．
于是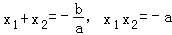
，
故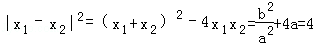
，
即b2=4a2﹣4a3．
由b2≥0得4a2﹣4a3≥0，解得a≤1．a＞0，
所以0＜a≤1得证．
（Ⅱ）由（Ⅰ）知b2=4a2﹣4a3，
设g（a）=4a2﹣4a3，
则g'（a）=8a﹣12a2=4a（2﹣3a）．
由g'（a）＞0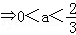
；g'（a）＜0
．
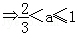故g（a）在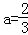
时取得最大值
，
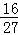即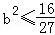
，
所以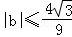
．
因为x1，x2是f（x）的两个极值点，
所以x1，x2是方程f'（x）=0的两个实根．
于是
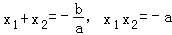，故
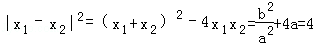，即b2=4a2﹣4a3．
由b2≥0得4a2﹣4a3≥0，解得a≤1．a＞0，
所以0＜a≤1得证．
（Ⅱ）由（Ⅰ）知b2=4a2﹣4a3，
设g（a）=4a2﹣4a3，
则g'（a）=8a﹣12a2=4a（2﹣3a）．
由g'（a）＞0
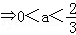；g'（a）＜0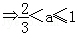．故g（a）在
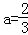时取得最大值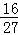，即
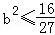，所以
．
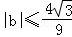练习册系列答案
相关题目
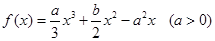的两个极值点，且
。
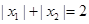，并求出a的取值范围.
.
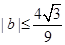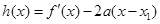,证明:当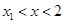
且x1<0时, 
.
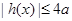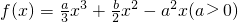的两个极值点，且|x1|+|x2|=2．
．
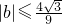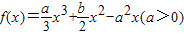的两个极值点，且|x1-x2|=2．
．
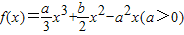的两个极值点，且|x1-x2|=2．
．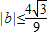