题目内容
已知函数 ,点
,点 在函数
在函数 的图象上,过P点的切线方程为
的图象上,过P点的切线方程为 .
.
(1)若 在
在 时有极值,求
时有极值,求 的解析式;
的解析式;
(2)在(1)的条件下是否存在实数m,使得不等式 m在区间
m在区间 上恒成立,若存在,试求出m的最大值,若不存在,试说明理由。
上恒成立,若存在,试求出m的最大值,若不存在,试说明理由。
【答案】
解:(1)∵ 是方程
是方程 的根,
的根,

又切线的斜率,即 在
在 时的值,
时的值,

点P既在函数 的图象上,又在切线
的图象上,又在切线 上,
上,
 ,解得
,解得
故
(2)在(1)的条件下,
由 得函数的两个极值点是
得函数的两个极值点是 .
.
函数的两个极值为
函数在区间的两个端点值分别为 .
.
比较极值与端点的函数值,知在区间 上,函数
上,函数 的最小值为
的最小值为 .
.
只需 ,不等式
,不等式 恒成立。此时
恒成立。此时 的最大值为
的最大值为
【解析】略

练习册系列答案
相关题目
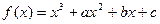 ,点
,点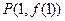 在函数
在函数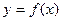 的图象上,过P点的切线方程为
的图象上,过P点的切线方程为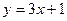 .
.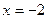 时有极值,求
时有极值,求 的解析式;
的解析式;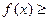 m在区间
m在区间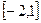 上恒成立,若存在,试求出m的最大值,若不存在,试说明理由。
上恒成立,若存在,试求出m的最大值,若不存在,试说明理由。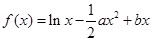 (
(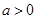 ),且
),且 .
.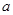 的式子表示
的式子表示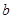 ,并求
,并求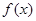 的极值;
的极值;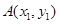 ,
,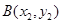 ,如果在函数图象上
,如果在函数图象上 存在点
存在点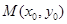 (其中
(其中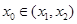 ),使得点
),使得点 处的切线
处的切线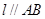 ,则称
,则称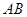 存在“伴随切线”. 特别地,当
存在“伴随切线”. 特别地,当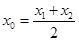 时,又称
时,又称 、
、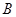 使得它存在“中值伴随切线”,若存在,求出
使得它存在“中值伴随切线”,若存在,求出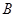 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.