题目内容
如图,正方形场地ABCD边长为200 m,在A附近已先占用以A为圆心以100 m为半径的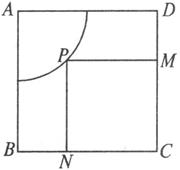
圆的场地,今要在余下场地上建一矩形楼房,使矩形两边分别在BC和CD上,问:这幢楼房的最大占地面积是多少平方米?
解：连结AP,延长MP交AB于Q,设∠PAQ=θ(0°≤θ≤90°),
则AQ=100cosθ,PQ=100sinθ.
∴PN=200-100cosθ,PM=200-100sinθ.
∴S=PN·PM=(200-100cosθ)(200-100sinθ)
=10 000［4-2(sinθ+cosθ)+sinθcosθ］.
设t=sinθ+cosθ(1≤t≤
),
则sinθcosθ=,
S=10 000(4-2t+
)=5 000(t-2)2+15 000.
当t=1时,S的最大值为20 000 m2.
答:这幢楼房的最大占地面积是20 000 m2.
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
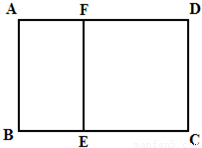
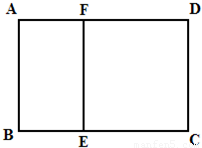
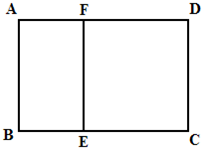如图，某单位准备修建一个面积为600平方米和矩形场地（图中ABCD）的围墙，且要求中间用围墙EF隔开，使得ABEF为矩形，EFCD为正方形，设AB=x米，已知围墙（包括EF）的修建费用均为800元每平方米，设围墙（包括EF）的修建总费用为y元．
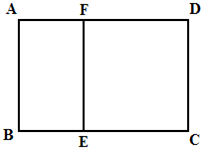如图，某单位准备修建一个面积为600平方米和矩形场地（图中ABCD）的围墙，且要求中间用围墙EF隔开，使得ABEF为矩形，EFCD为正方形，设AB=x米，已知围墙（包括EF）的修建费用均为800元每平方米，设围墙（包括EF）的修建总费用为y元．
