题目内容
数列{an}的前n项和为Sn,且Sn= (an-l),数列{bn}满足bn=
(an-l),数列{bn}满足bn=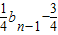 (n≥2),b1=3.
(n≥2),b1=3.(1)求数列{an}与{bn}的通项公式.
(2)设数列{cn} 满足cn=anlog2(bn+1),其前n项和为Tn,求Tn.
【答案】分析:(1)利用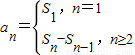 即可得出an;对于数列{bn}满足bn=
即可得出an;对于数列{bn}满足bn=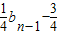 (n≥2),变形可得
(n≥2),变形可得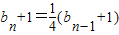 .利用等比数列的通项公式即可得出.
.利用等比数列的通项公式即可得出.
(2)利用“错位相减法”即可得出.
解答:解:(1)对于数列{an},当n=1时,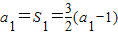 ,解得a1=3.
,解得a1=3.
当n≥2时,an=Sn-Sn-1=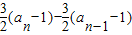 ,化为an=3an-1.
,化为an=3an-1.
∴数列{an}是首项为3,公比为3的等比数列,
∴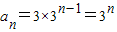 .
.
对于数列{bn}满足bn=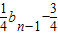 (n≥2),b1=3.
(n≥2),b1=3.
可得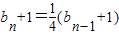 .
.
∴数列{bn+1}是以b1+1=4为首项, 为公比的等比数列.
为公比的等比数列.
∴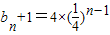 ,化为
,化为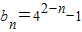 .
.
(2)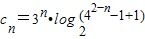 =3n(4-2n)
=3n(4-2n)
∴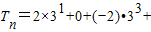 …+(4-2n)•3n.
…+(4-2n)•3n.
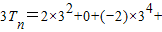 …+(6-2n)•3n+(4-2n)•3n+1.
…+(6-2n)•3n+(4-2n)•3n+1.
∴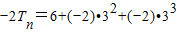 +…+(-2)•3n-(4-2n)•3n+1
+…+(-2)•3n-(4-2n)•3n+1
=6-2×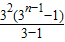 -(4-2n)•3n+1.
-(4-2n)•3n+1.
∴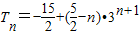 .
.
点评:熟练掌握利用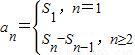 即可得出an;变形利用等比数列的通项公式、“错位相减法”、等比数列的前n项和公式等是解题的关键.
即可得出an;变形利用等比数列的通项公式、“错位相减法”、等比数列的前n项和公式等是解题的关键.
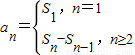 即可得出an;对于数列{bn}满足bn=
即可得出an;对于数列{bn}满足bn=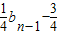 (n≥2),变形可得
(n≥2),变形可得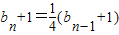 .利用等比数列的通项公式即可得出.
.利用等比数列的通项公式即可得出.(2)利用“错位相减法”即可得出.
解答:解:(1)对于数列{an},当n=1时,
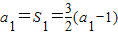 ,解得a1=3.
,解得a1=3.当n≥2时,an=Sn-Sn-1=
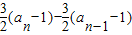 ,化为an=3an-1.
,化为an=3an-1.∴数列{an}是首项为3,公比为3的等比数列,
∴
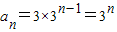 .
.对于数列{bn}满足bn=
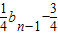 (n≥2),b1=3.
(n≥2),b1=3.可得
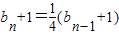 .
.∴数列{bn+1}是以b1+1=4为首项,
 为公比的等比数列.
为公比的等比数列.∴
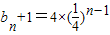 ,化为
,化为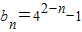 .
.(2)
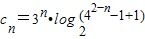 =3n(4-2n)
=3n(4-2n)∴
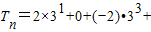 …+(4-2n)•3n.
…+(4-2n)•3n.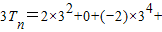 …+(6-2n)•3n+(4-2n)•3n+1.
…+(6-2n)•3n+(4-2n)•3n+1.∴
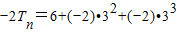 +…+(-2)•3n-(4-2n)•3n+1
+…+(-2)•3n-(4-2n)•3n+1=6-2×
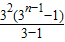 -(4-2n)•3n+1.
-(4-2n)•3n+1.∴
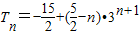 .
.点评:熟练掌握利用
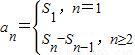 即可得出an;变形利用等比数列的通项公式、“错位相减法”、等比数列的前n项和公式等是解题的关键.
即可得出an;变形利用等比数列的通项公式、“错位相减法”、等比数列的前n项和公式等是解题的关键. 
练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目