题目内容
设命题p:曲线y=e-x在点(-1,e)处的切线方程是:y=-ex;命题q:a,b是任意实数,若a>b,则
<
.则( )
| 1 |
| a+1 |
| 1 |
| b+1 |
| A.“p或q”为真 | B.“p且q”为真 |
| C.p假q真 | D.p,q均为假命题 |
命题p:y′=-e-x则y′|x=-1=-e
∴曲线y=e-x在点(-1,e)处的切线方程是y-e=-e(x+1)即y=-ex
故命题p为真命题
命题q:2>-2而
>
,故命题q是假命题
根据复合命题的真假的真值表可知“p或q”为真,“p且q”为假
故选A.
∴曲线y=e-x在点(-1,e)处的切线方程是y-e=-e(x+1)即y=-ex
故命题p为真命题
命题q:2>-2而
| 1 |
| 2+1 |
| 1 |
| -2+1 |
根据复合命题的真假的真值表可知“p或q”为真,“p且q”为假
故选A.

练习册系列答案
相关题目
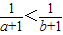 .则( )
.则( )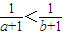 .则( )
.则( ) .则( )
.则( )