题目内容
边长为1的等边三角形ABC中,设
=
,
=
,
=
,则
•
+
•
+
=( )
| AB |
| c |
| BC |
| a |
| CA |
| b |
| a |
| b |
| b |
| c |
| c• |
| a |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
分析:由题设知
和
,
和
,
和
的夹角都是120°,|
|=|
|=|
|=1,由向量的数量积公式能够求解
•
+
•
+
.
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| c• |
| a |
解答:解:∵边长为1的等边三角形ABC中,
=
,
=
,
=
,
∴
•
+
•
+
=1×1×cos120°+1×1×cos120°+1×1×cos120°
=-
.
故选D.
| AB |
| c |
| BC |
| a |
| CA |
| b |
∴
| a |
| b |
| b |
| c |
| c• |
| a |
=1×1×cos120°+1×1×cos120°+1×1×cos120°
=-
| 3 |
| 2 |
故选D.
点评:本题考查向量的数量积公式的运用,解题时要注意
和
,
和
,
和
的夹角都是120°,|
|=|
|=|
|=1.
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| c |

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
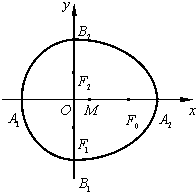 附加题:已知半椭圆
附加题:已知半椭圆 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
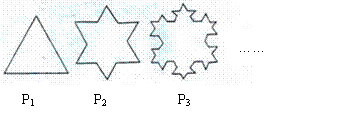
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求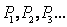 ,已知
,已知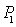 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对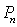 进行如下操作得到:将
进行如下操作得到:将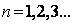 ).
).
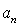 和
和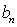 (
(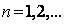 ),求
),求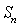 为曲线
为曲线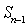 的递推关系式,并求
的递推关系式,并求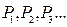 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对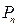 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求