题目内容
函数 的单调增区间是( )
的单调增区间是( )A.
 (k∈z)
(k∈z)B.
 (k∈z)
(k∈z)C.
 (k∈z)
(k∈z)D.
 (k∈z)
(k∈z)
【答案】分析:由于f(x)=-sin(2x-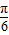 ),求得函数g(x)=sin(2x-
),求得函数g(x)=sin(2x-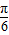 )的递减区间即为所求答案.
)的递减区间即为所求答案.
解答:解:∵f(x)=sin(-2x+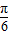 )=-sin(2x-
)=-sin(2x-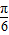 ),
),
令g(x)=sin(2x-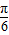 ),
),
则g(x)=sin(2x-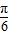 )的递减区间就是f(x)=sin(-2x+
)的递减区间就是f(x)=sin(-2x+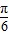 )的单调增区间.
)的单调增区间.
∴由2kπ-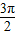 ≤2x-
≤2x-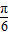 ≤2kπ-
≤2kπ-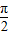 ,k∈Z得:
,k∈Z得:
kπ-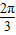 ≤x≤kπ-
≤x≤kπ-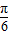 ,k∈Z
,k∈Z
∴f(x)=sin(-2x+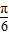 )的单调增区间为[kπ-
)的单调增区间为[kπ-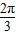 ,kπ-
,kπ-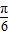 ](k∈Z).
](k∈Z).
故选B.
点评:本题考查复合三角函数的单调性,求g(x)=sin(2x-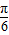 )的递减区间是关键,考查转化思想与计算能力,属于中档题.
)的递减区间是关键,考查转化思想与计算能力,属于中档题.
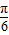 ),求得函数g(x)=sin(2x-
),求得函数g(x)=sin(2x-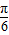 )的递减区间即为所求答案.
)的递减区间即为所求答案.解答:解:∵f(x)=sin(-2x+
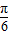 )=-sin(2x-
)=-sin(2x-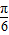 ),
),令g(x)=sin(2x-
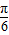 ),
),则g(x)=sin(2x-
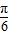 )的递减区间就是f(x)=sin(-2x+
)的递减区间就是f(x)=sin(-2x+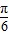 )的单调增区间.
)的单调增区间.∴由2kπ-
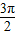 ≤2x-
≤2x-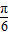 ≤2kπ-
≤2kπ-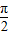 ,k∈Z得:
,k∈Z得:kπ-
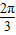 ≤x≤kπ-
≤x≤kπ-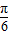 ,k∈Z
,k∈Z∴f(x)=sin(-2x+
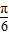 )的单调增区间为[kπ-
)的单调增区间为[kπ-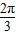 ,kπ-
,kπ-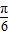 ](k∈Z).
](k∈Z).故选B.
点评:本题考查复合三角函数的单调性,求g(x)=sin(2x-
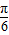 )的递减区间是关键,考查转化思想与计算能力,属于中档题.
)的递减区间是关键,考查转化思想与计算能力,属于中档题. 
练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 的单调增区间是
的单调增区间是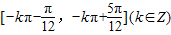 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动 个单位长度.
个单位长度. .
. 的单调增区间是 .
的单调增区间是 . 的单调增区间是
的单调增区间是 B.
B. C.
C. D.
D.
 的单调增区间是___________________________。
的单调增区间是___________________________。