题目内容
已知函数f(x)=sin2ωx+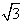 sinωxsin(ωx+
sinωxsin(ωx+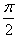 )(ω>0)的最小正周期为π,
)(ω>0)的最小正周期为π,
(Ⅰ)求f(x)的单调增区间并写出f(x)图象的对称中心的坐标;
(Ⅱ)求函数f(x)在区间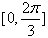 上的最大值与最小值。
上的最大值与最小值。
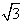 sinωxsin(ωx+
sinωxsin(ωx+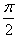 )(ω>0)的最小正周期为π,
)(ω>0)的最小正周期为π,(Ⅰ)求f(x)的单调增区间并写出f(x)图象的对称中心的坐标;
(Ⅱ)求函数f(x)在区间
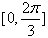 上的最大值与最小值。
上的最大值与最小值。解:(Ⅰ)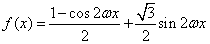
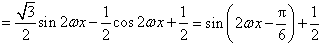 ,
,
因为函数f(x)的最小正周期为π,且ω>0,
所以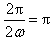 ,解得ω=1,
,解得ω=1,
∴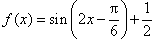 ,
,
所以f(x)的单调增区间为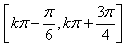 (k∈Z),
(k∈Z),
f(x)图象的对称中心的坐标为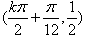 (k∈Z);
(k∈Z);
(Ⅱ)由(Ⅰ)得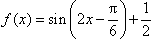 ,
,
因为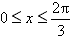 ,
,
所以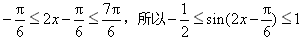 ,
,
因此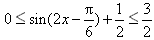
,
即f(x)的最大值为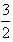 ,最小值为0。
,最小值为0。
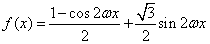
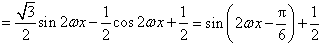 ,
,因为函数f(x)的最小正周期为π,且ω>0,
所以
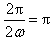 ,解得ω=1,
,解得ω=1, ∴
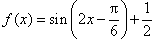 ,
,所以f(x)的单调增区间为
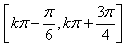 (k∈Z),
(k∈Z),f(x)图象的对称中心的坐标为
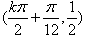 (k∈Z);
(k∈Z);(Ⅱ)由(Ⅰ)得
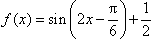 ,
,因为
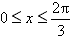 ,
,所以
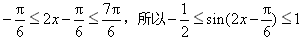 ,
,因此
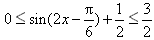
即f(x)的最大值为
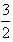 ,最小值为0。
,最小值为0。
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
