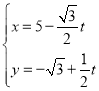Question

【题目】已知F1，F2是椭圆C：（a＞b＞0）的左、右焦点，过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为.

（Ⅰ）求椭圆C的方程；

（Ⅱ）过F1的直线l交椭圆于A，B两点，当△ABF2面积最大时，求直线l的方程.

Answer 1

【答案】（Ⅰ）y2=1；（Ⅱ）x﹣y0或x+y0.

【解析】

（Ⅰ）根据直线椭圆的过上顶点，得b=1，再利用点差法以及弦中点坐标解得a2=3，即得椭圆方程；

（Ⅱ）先设直线l方程并与椭圆方程联立，结合韦达定理，并以|F1F2|为底边长求△ABF2面积函数关系式，在根据基本不等式求△ABF2面积最大值，进而确定直线l的方程.

（Ⅰ）直线x+y=1与y轴的交于（0，1）点，∴b=1，

设直线x+y=1与椭圆C交于点M（x1，y1），N（x2，y2），

则x1+x2，y1+y2，

∴1，1，

两式相减可得（x1﹣x2）（x1+x2）（y1﹣y2）（y1+y2）=0，

∴，

∴ 1，

解得a2=3，

∴椭圆C的方程为y2=1.

（Ⅱ）由（Ⅰ）可得F1（，0），F2（，0），设A（x3，y3），B（x4，y4），

可设直线l的方程x=my，将直线l的方程x=my代入y2=1，可得（m2+3）y2﹣2my﹣1=0，

则y3+y4，y3y4，

|y3﹣y4|，

∴|F1F2||y3﹣y4|||y3﹣y4|，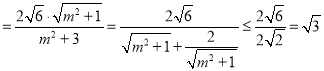

当且仅当，即m=±1，△ABF2面积最大，

即直线l的方程为x﹣y0或x+y0.