Question

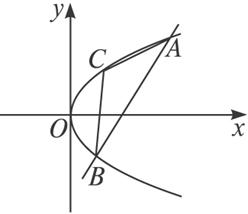
已知抛物线y²=4x截直线y=2x+b所得的弦长为AB=3 cm,

(1)求实数b的值;

(2)当点C在此抛物线上，且△ABC的面积为12 cm²时，求点C的坐标.

Answer 1

解：(1)如图，联立方程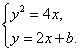

∴4x²+(4b-4)x+b²=0,由弦长公式l=,可得

3=.

∴b=-4.

(2)设C（,t）.

∴C到y=2x-4的距离为d=.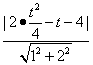

又|AB|=3,S_△ABC=|AB|·d,

∴12=×3×.

∴|t²-t-4|=8.

∴t²-t-4=8或t²-t-4=-8(无解）.

∴t=6或-4.

故C点坐标为（9，6）或（4，-4）.