题目内容
已知函数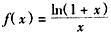
，
(Ⅰ)确定y=f(x)在(0，+∞)上的单调性；
(Ⅱ)设h(x)=x·f(x)-x-ax3在(0，2)上有极值，求a的取值范围。
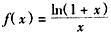，(Ⅰ)确定y=f(x)在(0，+∞)上的单调性；
(Ⅱ)设h(x)=x·f(x)-x-ax3在(0，2)上有极值，求a的取值范围。
解：(Ⅰ)由已知函数求导得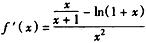
，
设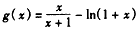
，
则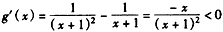
，
∴
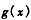在
上递减，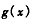
，
∴
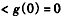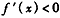，因此f（x）在
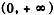上单调递减。
(Ⅱ)由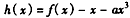
可得，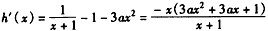
，
若a≥0，任给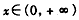
，
，
∴
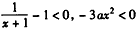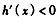，h（x）在（0，2）上单调递减，则f（x）在（0，2）上无极值，
若a＜0，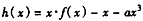
在（0，2）上有极值的充要条件是
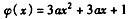在（0，2）上有零点，
∴
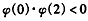，解得：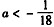
，
综上，a的取值范围是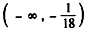
。
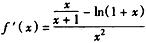，设
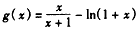，则
，∴
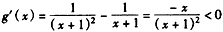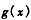在上递减，，∴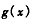
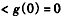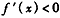，因此f（x）在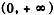上单调递减。(Ⅱ)由
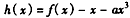可得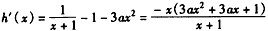，，若a≥0，任给
，，∴
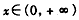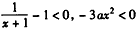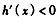，h（x）在（0，2）上单调递减，则f（x）在（0，2）上无极值，若a＜0，
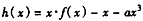在（0，2）上有极值的充要条件是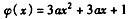在（0，2）上有零点，∴
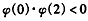，解得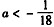：，综上，a的取值范围是
。
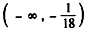练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
(
) , (Ⅰ)试确定
的单调区间 , 并证明你的结论 ;(Ⅱ)若
时 , 不等式
恒成立 , 求实数
的取值范围 . 
.
个单位长度，所得图象关于y轴对称，求φ的值。
．
的值，使
为奇函数；
，求
的取值范围．