题目内容
(本小题满分12分)
设数列 的前
的前 项和为
项和为 已知
已知

(1)设 ,证明数列
,证明数列 是等比数列;
是等比数列;
(2)求数列 的通项公式;
的通项公式;
 (3)若
(3)若 ,
, 为
为 的前n项和,求证:
的前n项和,求证:
 .
.
设数列
 的前
的前 项和为
项和为 已知
已知

(1)设
 ,证明数列
,证明数列 是等比数列;
是等比数列;(2)求数列
 的通项公式;
的通项公式; (3)若
(3)若 ,
, 为
为 的前n项和,求证:
的前n项和,求证:
 .
.(1)

(2)略
解:(I)由 及
及 ,有
,有


由 ,...① 则当
,...① 则当 时,有
时,有 .....②
.....②
②-①得
又 ,
,
 是首项
是首项 ,公比为2的等比数列.…….4分
,公比为2的等比数列.…….4分
(II)由(I)可得 ,
,
 数列
数列 是首项为
是首项为 ,公差为
,公差为 的等差数列.
的等差数列.

 ,
, …….8分
…….8分
(Ⅲ)
所以 =
= ………12分
………12分
 及
及 ,有
,有

由
 ,...① 则当
,...① 则当 时,有
时,有 .....②
.....②②-①得

又
 ,
,
 是首项
是首项 ,公比为2的等比数列.…….4分
,公比为2的等比数列.…….4分(II)由(I)可得
 ,
,
 数列
数列 是首项为
是首项为 ,公差为
,公差为 的等差数列.
的等差数列.
 ,
, …….8分
…….8分(Ⅲ)

所以
 =
= ………12分
………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
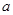 元,若每到第二年的这一天取出,再连本带利存入银行(假设银行年利率为
元,若每到第二年的这一天取出,再连本带利存入银行(假设银行年利率为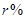 ),则到2015年1月5日他共可取出款
),则到2015年1月5日他共可取出款 (元)
(元)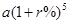 (元)
(元) (元)
(元)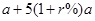 (元)
(元) 中,首项
中,首项 ,前三项和为
,前三项和为 ,则
,则 =
=



 为等比数列”是“数列
为等比数列”是“数列 为等比数列”的
为等比数列”的 是互
是互 异的正数,
异的正数, 是
是 是
是 )选填其中一个.
)选填其中一个. 是首项为1的等比数列,
是首项为1的等比数列, 是
是 ,则数列
,则数列 的前5项和为
的前5项和为  的前n项和为Sn,若S3=2,S6=18,则
的前n项和为Sn,若S3=2,S6=18,则 等于( )
等于( )
 31
31