题目内容
如图,已知正方形ABCD与矩形BEFD所在的平面互相垂直,AB=2,DF=1,P是线段EF上的动点.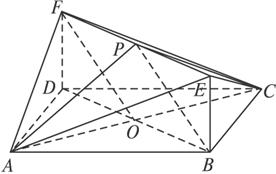
(1)若点O为正方形ABCD的中心,求直线OP与平面ABCD所成角的最大值;
(2)在点P为EF的中点时,求直线BP与FA所成角的正弦值;
(3)求二面角AEFC的大小.
解:(1)连结OP.设OP与平面ABCD所成角为α,则α∈[![]() ,
,![]() ].当P是线段EF的中点时,OP⊥平面ABCD,直线OP与平面ABCD所成的最大角是
].当P是线段EF的中点时,OP⊥平面ABCD,直线OP与平面ABCD所成的最大角是![]() .
.

(2)连结AF、FC、OF.
易证FO∥PB,∴∠AFO是直线BP与FA所成的角.
依题意,在等腰△AFC中,FO⊥AC,△AOF为直角三角形.
∵AD=![]() ,DF=1,∴AF=
,DF=1,∴AF=![]() .
.
又AO=![]()
![]() =1,
=1,
∴在Rt△AOF中,sin∠AFO=![]() .
.
(3)连结AE、EC,则AF=FC=AE=EC=![]() .取EF的中点P,连结AP、CP,则AP⊥EF,CP⊥EF,
.取EF的中点P,连结AP、CP,则AP⊥EF,CP⊥EF,
∴∠APC是二面角AEFC的平面角.
等腰△AEF≌△CEF,∴在△APC中,AP=CP=![]() .
.
又AC=2,∴△APC是直角三角形,且∠APC=![]() .
.
∴二面角AEFC的大小是![]() .
.

练习册系列答案
相关题目
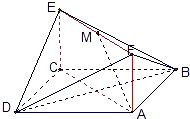 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= 如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当
如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.