题目内容
(本小题满分12分)
已知数列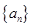 的前
的前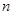 项和为
项和为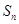 ,且对任意正整数
,且对任意正整数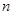 ,都有
,都有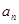 是
是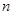 与
与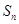 的等差中项.
的等差中项.
(1)求证:数列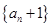 为等比数列;
为等比数列;
(2)求数列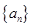 的前
的前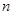 项和
项和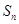 .
.
【答案】
(1)证明:
 是
是 与
与 的等差中项,
的等差中项,
 ①
①
于是 ②
②
①-②得 ,即
,即 ,
,
当 时
时 ,
, .
.
所以 是以2为首项,2为公比的等比数列. …………………6分
是以2为首项,2为公比的等比数列. …………………6分
(2)
 .
……………………12分
.
……………………12分
【解析】略

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目