题目内容
已知函数 f(2x)
f(2x)
(I)用定义证明函数 在
在 上为减函数。
上为减函数。
(II)求 在
在 上的最小值.
上的最小值.
(I)见解析(II)-3
解析试题分析:(I)先求出 的解析式,再根据函数单调性的定义证明:第一步,在所给区间内任取两个自变量的值
的解析式,再根据函数单调性的定义证明:第一步,在所给区间内任取两个自变量的值 且
且 ;第二步,比较
;第二步,比较 的大小;第三步,下结论.
的大小;第三步,下结论.
(II)利用函数单调性 在
在 的单调性求出最小值.
的单调性求出最小值.
试题解析:解:(I)
又 ∴函数
∴函数 的定义域
的定义域 , 3分
, 3分
设 且
且
 6分
6分 且
且 ,
,
∴ 且
且
根据函数单调性的定义知:函数 在
在 上为减函数. 8分
上为减函数. 8分
(II)∵ :函数 在
在 上为减函数,∴:函数
上为减函数,∴:函数 在
在 上为减函数,
上为减函数,
∴当x=-1时, 12分
12分
考点:1、函数的单调性定义;2、函数单调性的应用.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ;
; ;
; ;
; .
. 上的函数
上的函数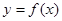 是偶函数,且
是偶函数,且 时,
时,  。
。 时,求
时,求 解析式;
解析式; ,求
,求 取值的集合;
取值的集合; ,函数的值域为
,函数的值域为 ,求
,求 满足的条件
满足的条件  若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立. (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1.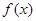 的单调区间,
的单调区间,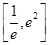 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围. 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围.
的取值范围. 上的函数
上的函数 同时满足以下条件:
同时满足以下条件: 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数; 是偶函数;
是偶函数; y=x+2垂直.
y=x+2垂直. =
= ,若存在实数x∈[1,e],使
,若存在实数x∈[1,e],使 <
< .
. 为偶函数,求
为偶函数,求 的值;
的值; ,求函数
,求函数 时,若对任意的
时,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 ,x∈[1,3],
,x∈[1,3], 于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围.
于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围.