题目内容
已知等比数列{an}为递增数列,且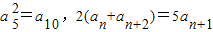 ,则数列an的通项公式an= .
,则数列an的通项公式an= .
【答案】分析:通过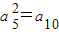 ,求出等比数列的首项与公比的关系,通过2(an+an+2)=5an+1求出公比,推出数列的通项公式即可.
,求出等比数列的首项与公比的关系,通过2(an+an+2)=5an+1求出公比,推出数列的通项公式即可.
解答:解:∵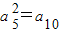 ,∴
,∴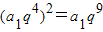 ,
,
∴a1=q,
∴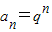 ,
,
∵2(an+an+2)=5an+1,
∴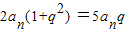 ,
,
∴2(1+q2)=5q,
解得q=2或q= (等比数列{an}为递增数列,舍去)
(等比数列{an}为递增数列,舍去)
∴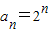 .
.
故答案为:2n.
点评:本题主要考查等比数列的通项公式,转化思想和逻辑推理能力,属于中档题.
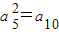 ,求出等比数列的首项与公比的关系,通过2(an+an+2)=5an+1求出公比,推出数列的通项公式即可.
,求出等比数列的首项与公比的关系,通过2(an+an+2)=5an+1求出公比,推出数列的通项公式即可.解答:解:∵
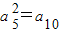 ,∴
,∴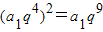 ,
,∴a1=q,
∴
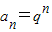 ,
,∵2(an+an+2)=5an+1,
∴
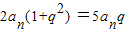 ,
,∴2(1+q2)=5q,
解得q=2或q=
 (等比数列{an}为递增数列,舍去)
(等比数列{an}为递增数列,舍去)∴
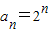 .
.故答案为:2n.
点评:本题主要考查等比数列的通项公式,转化思想和逻辑推理能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目