题目内容
已知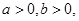 且
且 ,若
,若 恒成立,
恒成立,
(1)求 的最小值;(2)若
的最小值;(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
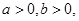 且
且 ,若
,若 恒成立,
恒成立,(1)求
 的最小值;(2)若
的最小值;(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.(1)3;(2) 或
或
 或
或
试题分析:(1)
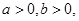 且
且 ,若
,若 恒成立.即要求出
恒成立.即要求出 的最大值.由柯西不等式可求得.
的最大值.由柯西不等式可求得.(2)因为
 对任意的
对任意的 恒成立.所以等价于
恒成立.所以等价于 的最大值小于或等于
的最大值小于或等于 .由(1)可得
.由(1)可得 .所以等价于
.所以等价于 恒成立.通过讨论即求得x的范围.本小题的关键是关于恒成立的问题的正确理解.
恒成立.通过讨论即求得x的范围.本小题的关键是关于恒成立的问题的正确理解.试题解析:(1)
 ,
, ,(当且仅当
,(当且仅当 ,即
,即 时取等号)
时取等号)又∵
 恒成立,∴
恒成立,∴ .
.故
 的最小值为3.
的最小值为3. (2)要使
 恒成立,须且只须
恒成立,须且只须 .
.∴
 或
或 或
或
∴
 或
或 .
.
练习册系列答案
相关题目
 ,m∈R,且
,m∈R,且 的解集为
的解集为 .
. 的值;
的值; +,且
+,且 ,求
,求 的最小值.
的最小值. ,不等式
,不等式 的解集为
的解集为 .
. 的值;
的值; 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数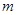 的取值范围.
的取值范围. +
+ +
+ 的最小值为 ( )
的最小值为 ( )
 ,若存在
,若存在 ,使得任意
,使得任意 恒成立,且两边等号能取到,则
恒成立,且两边等号能取到,则 的最小值为 .
的最小值为 . +
+ ,Q=
,Q= +
+ (a≥0),则P、Q的大小关系是( )
(a≥0),则P、Q的大小关系是( ) 恒成立,则n的最大值为( ).
恒成立,则n的最大值为( ). a∨b=
a∨b=