题目内容
(不等式选讲)用max{x,y,z}表示x,y,z三个实数中的最大数,对于任意实数a,b,设max{|a|,|a+b+1|,|a-b+1|}=M,则M的最小值是________.

分析:由已知中max{x,y,z}表示x,y,z三个实数中的最大数,若max{|a|,|a+b+1|,|a-b+1|}=M,则M≥|a|且M≥|a+b+1|且M≥|a-b+1|,结合绝对值不等式的性质,可得4M≥|-2a+a+b+1+a-b+1|=2,进而求出答案.
解答:∵max{|a|,|a+b+1|,|a-b+1|}=M
∴M≥|a|且M≥|a+b+1|且M≥|a-b+1|
即M≥|-a|且M≥|a+b+1|且M≥|a-b+1|
故4M≥|-2a+a+b+1+a-b+1|=2
故M≥

即M的最小值是

故答案为:

点评:本题考查的知识点是函数的最值及其几何意义,绝对值的性质,其中利用|A+B|≤|A|+|B|求出M的范围是解答的关键.

练习册系列答案
相关题目
 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。
 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线

 的图象;
的图象; 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。
 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线

 的图象;
的图象; 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。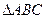 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。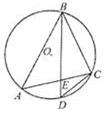
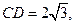 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。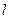 的参数方程为
的参数方程为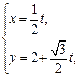 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为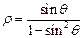 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线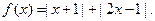
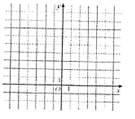
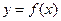 的图象;
的图象;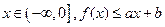 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。