题目内容
一个圆的极坐标方程是ρ=2sin(θ+
),则圆心的极坐标是( )
| π |
| 4 |
分析:把圆的极坐标方程化为直角坐标系下的标准方程,求出圆心坐标,再把它化为极坐标.
解答:解:圆 ρ=2sin(θ+
)=
(cosθ+sinθ)
即 ρ2=
(ρcosθ+ρsinθ),它的直角坐标方程为
(x-
)2+(y-
)2=1,表示以A(
,
)为圆心的圆,
A到极点的距离等于1,与极轴的夹角等与
,
故圆心的极坐标是 (1,
),
故选 A.
| π |
| 4 |
| 2 |
即 ρ2=
| 2 |
(x-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
A到极点的距离等于1,与极轴的夹角等与
| π |
| 4 |
故圆心的极坐标是 (1,
| π |
| 4 |
故选 A.
点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,等进行代换即得.

练习册系列答案
相关题目
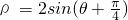 ,则圆心的极坐标是
,则圆心的极坐标是



 ,则圆心的极坐标是( )
,则圆心的极坐标是( )


