题目内容
已知数列{an}满足: (n∈N*,a∈R,a为常数),数列{bn}中,
(n∈N*,a∈R,a为常数),数列{bn}中,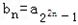 .
.
(1)求a1,a2,a3;
(2)证明:数列{bn}为等差数列;
(3)求证:数列{bn}中存在三项构成等比数列时,a为有理数.
 (n∈N*,a∈R,a为常数),数列{bn}中,
(n∈N*,a∈R,a为常数),数列{bn}中,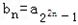 .
.(1)求a1,a2,a3;
(2)证明:数列{bn}为等差数列;
(3)求证:数列{bn}中存在三项构成等比数列时,a为有理数.
解:(1)由已知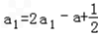 ,得
,得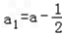 ,
,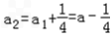 ,
,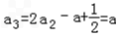 .
.
(2)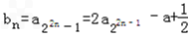 ,
,
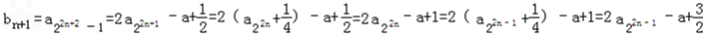 ∴bn+1﹣bn=1,又b1=a3=a,
∴bn+1﹣bn=1,又b1=a3=a,
∴数列{bn}是首项为a,公差为1的等差数列.
(3)证明:由(2)知bn=a+n﹣1,
若三个不同的项a+i,a+j,a+k成等比数列,
i、j、k为非负整数,且i<j<k,
则(a+j)2=(a+i)(a+k),得a(i+k﹣2j)=j2﹣ik,
若i+k﹣2j=0,则j2﹣ik=0,得i=j=k,这与i<j<k矛盾.
若i+k﹣2j≠0,则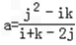 ,
,
∵i、j、k为非负整数,
∴a是有理数.
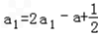 ,得
,得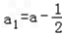 ,
,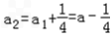 ,
,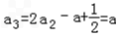 .
.(2)
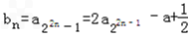 ,
,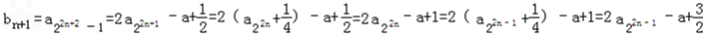 ∴bn+1﹣bn=1,又b1=a3=a,
∴bn+1﹣bn=1,又b1=a3=a, ∴数列{bn}是首项为a,公差为1的等差数列.
(3)证明:由(2)知bn=a+n﹣1,
若三个不同的项a+i,a+j,a+k成等比数列,
i、j、k为非负整数,且i<j<k,
则(a+j)2=(a+i)(a+k),得a(i+k﹣2j)=j2﹣ik,
若i+k﹣2j=0,则j2﹣ik=0,得i=j=k,这与i<j<k矛盾.
若i+k﹣2j≠0,则
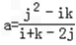 ,
, ∵i、j、k为非负整数,
∴a是有理数.

练习册系列答案
相关题目