题目内容
已知函数f(x)=x+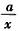 +lnx(a∈R),
+lnx(a∈R),
(Ⅰ)求函数f(x)的单调区间与极值点;
(Ⅱ)若对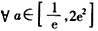 ,函数f(x)满足对
,函数f(x)满足对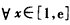 都有f(x)<m成立,求实数m的取值范围(其中e是自然对数的底数)。
都有f(x)<m成立,求实数m的取值范围(其中e是自然对数的底数)。
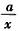 +lnx(a∈R),
+lnx(a∈R), (Ⅰ)求函数f(x)的单调区间与极值点;
(Ⅱ)若对
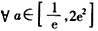 ,函数f(x)满足对
,函数f(x)满足对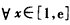 都有f(x)<m成立,求实数m的取值范围(其中e是自然对数的底数)。
都有f(x)<m成立,求实数m的取值范围(其中e是自然对数的底数)。 解:(Ⅰ)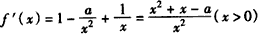 ,
,
①a≤0时,f′(x)≥0,f(x)在(0,+∞)上单调递增,此时函数 f(x)无极值点;
②a>0,令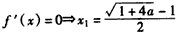 (
(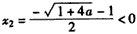 舍去),
舍去),
当0<x<x1时,f′(x)<0,f(x)在(0,x1)上单调递减;
当x>x1时,f′(x)>0,f(x)在(x1,+∞)上单调递增;
即f(x)在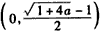 上单调递减,在
上单调递减,在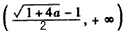 上单调递增,
上单调递增,
此时函数f(x)仅有极小值点 。
。
(Ⅱ)函数f(x)满足: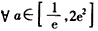 ,对
,对 都有f(x)<m成立,
都有f(x)<m成立,
即f(x)在[1,e]上的最大值小于m,
由(Ⅰ)知, ,f(x)在
,f(x)在 上单调递减,在
上单调递减,在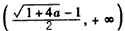 上单调递增,
上单调递增,
所以, 对
对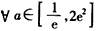 恒成立
恒成立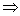
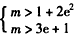 ,
,
又1+2e2-(3e+l)=(2e-3)e>0 1+2e2>3e+l,
1+2e2>3e+l,
故实数m的取值范围是(1+2e2,+∞)。
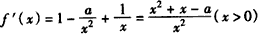 ,
,①a≤0时,f′(x)≥0,f(x)在(0,+∞)上单调递增,此时函数 f(x)无极值点;
②a>0,令
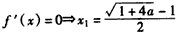 (
(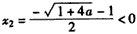 舍去),
舍去),当0<x<x1时,f′(x)<0,f(x)在(0,x1)上单调递减;
当x>x1时,f′(x)>0,f(x)在(x1,+∞)上单调递增;
即f(x)在
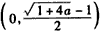 上单调递减,在
上单调递减,在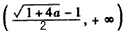 上单调递增,
上单调递增,此时函数f(x)仅有极小值点
 。
。 (Ⅱ)函数f(x)满足:
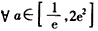 ,对
,对 都有f(x)<m成立,
都有f(x)<m成立,即f(x)在[1,e]上的最大值小于m,
由(Ⅰ)知,
 ,f(x)在
,f(x)在 上单调递减,在
上单调递减,在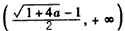 上单调递增,
上单调递增,所以,
 对
对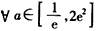 恒成立
恒成立
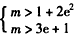 ,
,又1+2e2-(3e+l)=(2e-3)e>0
 1+2e2>3e+l,
1+2e2>3e+l,故实数m的取值范围是(1+2e2,+∞)。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目