题目内容
【题目】借助计算机(器)作某些分段函数图象时,分段函数的表示有时可以利用函数![]() ,例如要表示分段函数g(x)=
,例如要表示分段函数g(x)=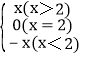 总可以将g(x)表示为g(x)=xh(x-2)+(-x)h(2-x).
总可以将g(x)表示为g(x)=xh(x-2)+(-x)h(2-x).
(1)设f(x)=(x2-2x+3)h(x-1)+(1-x2)h(1-x),请把函数f(x)写成分段函数的形式;
(2)已知G(x)=[(3a-1)x+4a]h(1-x)+logaxh(x-1)是R上的减函数,求a的取值范围;
(3)设F(x)=(x2+x-a+1)h(x-a)+(x2-x+a+1)h(a-x),求函数F(x)的最小值.
【答案】(1)f(x)=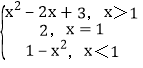 ; (2)
; (2)![]() ≤a<
≤a<![]() ; (3)当a≤-
; (3)当a≤-![]() 时,最小值为-a+
时,最小值为-a+![]() ;当a≥
;当a≥![]() 时,最小值为为a+
时,最小值为为a+![]() ;当-
;当-![]() <a<
<a<![]() 时,最小值为F(a)=a2+1.
时,最小值为F(a)=a2+1.
【解析】
(1)分当x>1、当x=1和当x<1时3种情况加以讨论,分别根据函数的对应法则代入,可得f(x)相应范围内的表达式,最后综合可得函数f(x)写成分段函数的形式;
(2)运用分段函数形式表示G(x),再由一次函数、对数函数的单调性,可得a的范围;
(3)由题意,讨论x>a,x=a,x<a,求得F(x)的解析式,再结合二次函数的图象与性质,分a![]() 、
、![]() a
a![]() 和a
和a![]() 的4种情况进行讨论,最后综合可得F(x)的最小值.
的4种情况进行讨论,最后综合可得F(x)的最小值.
(1)当x>1时,x-1>0,1-x<0,可得f(x)=(x2-2x+3)+0(1-x2)=x2-2x+3;
当x=1时,f(x)=2;
当x<1时,x-1<0,1-x>0,可得f(x)=1-x2.
即有f(x)=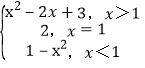 ;
;
(2)G(x)=[(3a-1)x+4a]h(1-x)+logaxh(x-1)
=![]() ,
,
由y=G(x)是R上的减函数,
可得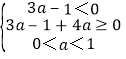 ,
,
解得![]() ≤a<
≤a<![]() ;
;
(3)F(x)=(x2+x-a+1)h(x-a)+(x2-x+a+1)h(a-x),
当x>a时,x-a>0,可得F(x)=x2+x-a+1;
若a≥-![]() ,可得F(x)在x>a递增,可得F(x)>F(a)=a2+1;
,可得F(x)在x>a递增,可得F(x)>F(a)=a2+1;
若a<-![]() ,可得F(x)的最小值为F(-
,可得F(x)的最小值为F(-![]() )=
)=![]() -a;
-a;
当x=a时,可得F(x)=2(a2+1);
当x<a时,x-a<0,a-x>0,则F(x)=x2-x+a+1.
若a≥![]() ,可得F(x)在x<a的最小值为F(
,可得F(x)在x<a的最小值为F(![]() )=a+
)=a+![]() ;
;
若a<![]() ,可得F(x)在x<a递减,即有F(x)>F(a)=a2+1.
,可得F(x)在x<a递减,即有F(x)>F(a)=a2+1.
①当a≥![]() 时,F(x)在区间(-∞,-
时,F(x)在区间(-∞,-![]() )上单调递减,
)上单调递减,
在区间(-![]() ,a)上单调递增,在区间(a,+∞)上单调递增,
,a)上单调递增,在区间(a,+∞)上单调递增,
可得F(-![]() )为最小值,且为
)为最小值,且为![]() -
-![]() +a+1=a+
+a+1=a+![]() ;
;
②当-![]() <a<
<a<![]() 时,F(x)在区间(-∞,a)上单调递减,在区间(a,+∞)上单调递增.
时,F(x)在区间(-∞,a)上单调递减,在区间(a,+∞)上单调递增.
F(x)的最小值为F(a)=a2+1;
③当a≤-![]() 时,在区间(-∞,a)上单调递减,在区间(a,-
时,在区间(-∞,a)上单调递减,在区间(a,-![]() )上单调递减,
)上单调递减,
在区间(-![]() ,+∞)上单调递增.
,+∞)上单调递增.
所以F(x)的最小值为F(-![]() )=-a+
)=-a+![]() ;
;
综上所述,得当a≤-![]() 时,F(x)的最小值为-a+
时,F(x)的最小值为-a+![]() ;
;
当a≥![]() 时,F(x)的最小值为为a+
时,F(x)的最小值为为a+![]() ;
;
当-![]() <a<
<a<![]() 时,F(x)的最小值为F(a)=a2+1.
时,F(x)的最小值为F(a)=a2+1.

