题目内容
已知函数![]() ,
,![]() ,其中
,其中![]() R .
R .
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() , 当
, 当![]() 时,若存在
时,若存在![]() ,对于任意的
,对于任意的![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
5. 解:(Ⅰ)![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ;
;
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)![]() ,
,![]() 的定义域为
的定义域为![]()
![]()
因为![]() 在其定义域内为增函数,所以
在其定义域内为增函数,所以![]() ,
,![]()
![]()
而 ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以![]()
(Ⅲ)当![]() 时,
时,![]() ,
,![]()
由![]() 得
得![]() 或
或![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以在![]() 上,
上,![]()
而“![]() ,
,![]() ,总有
,总有![]() 成立”等价于
成立”等价于
“![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() 在
在![]() 上的最大值”
上的最大值”
而![]() 在
在![]() 上的最大值为
上的最大值为![]()
所以有
![]()

![]()
所以实数![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目

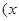 >
>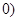 ,其中r为有理数,且0<r<1. 则
,其中r为有理数,且0<r<1. 则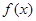 的最小值为_______;
的最小值为_______; .,其中a,b∈R
.,其中a,b∈R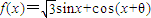 的定义域为R,最大值为1(其中θ为常数,且
的定义域为R,最大值为1(其中θ为常数,且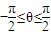 ).
).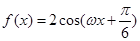 ,(其中
,(其中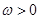 ,x∈R)的最小正周期为
,x∈R)的最小正周期为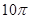 .
. ,
,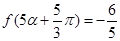 ,
,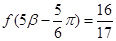 ,求
,求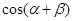 的值.
的值.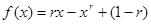
 >
>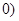 ,其中r为有理数,且0<r<1. 则
,其中r为有理数,且0<r<1. 则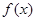 的最小值为_______;
的最小值为_______;