题目内容
设函数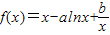 在x=1处取得极值.
在x=1处取得极值.(Ⅰ)求a与b满足的关系式;
(Ⅱ)若a>1,求函数f(x)的单调区间;
(Ⅲ)若a>3,函数g(x)=a2x2+3,若存在m1,
 ,使得|f(m1)-g(m2)|<9成立,求a的取值范围.
,使得|f(m1)-g(m2)|<9成立,求a的取值范围.
【答案】分析:(Ⅰ)求导函数,利用函数在x=1处取得极值,可得a与b满足的关系式;
(Ⅱ)确定函数f(x)的定义域,求导函数,确定分类标准,从而可得函数f(x)的单调区间;
(Ⅲ)当a>3时,确定f(x)在[ ,2]上的最大值,g(x)在[
,2]上的最大值,g(x)在[ ,2]上的最小值,要使存在m1,m2∈[
,2]上的最小值,要使存在m1,m2∈[ ,2],使得|f(m1)-g(m2)|<9成立,只需要|f(x)max-g(x)min|<9,即可求得a的取值范围.
,2],使得|f(m1)-g(m2)|<9成立,只需要|f(x)max-g(x)min|<9,即可求得a的取值范围.
解答:解:(Ⅰ)求导函数可得f′(x)=1- -
- ,…(2分)
,…(2分)
由f′(1)=0得b=1-a. …(3分)
(Ⅱ)函数f(x)的定义域为(0,+∞),…(4分)
由(Ⅰ)可得f′(x)=1- -
- =
= .
.
令f′(x)=0,则x1=1,x2=a-1. …(6分)
因为x=1是f(x)的极值点,所以x1≠x2,即a≠2. …(7分)
所以当a>2时,a-1>1,
所以单调递增区间为(0,1),(a-1,+∞),单调递减区间为(1,a-1). …(8分)
当1<a<2时,0<a-1<1,
所以单调递增区间为(0,a-1),(1,+∞),单调递减区间为(a-1,1). …(9分)
(Ⅲ)当a>3时,f(x)在[ ,1)上为增函数,在(1,2]为减函数,
,1)上为增函数,在(1,2]为减函数,
所以f(x)的最大值为f(1)=2-a<0. …(10分)
因为函数g(x)在[ ,2]上是单调递增函数,所以g(x)的最小值为g(
,2]上是单调递增函数,所以g(x)的最小值为g( )=
)= a2+3>0. …(11分)
a2+3>0. …(11分)
所以g(x)>f(x)在[ ,2]上恒成立. …(12分)
,2]上恒成立. …(12分)
要使存在m1,m2∈[ ,2],使得|f(m1)-g(m2)|<9成立,只需要g(
,2],使得|f(m1)-g(m2)|<9成立,只需要g( )-f(1)<9,即
)-f(1)<9,即 a2+3-(2-a)<9,
a2+3-(2-a)<9,
所以-8<a<4. …(13分)
又因为a>3,所以a的取值范围是(3,4). …(14分)
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,解题的关键是正确求导,确定分类标准,利用函数的最值解决恒成立问题.
(Ⅱ)确定函数f(x)的定义域,求导函数,确定分类标准,从而可得函数f(x)的单调区间;
(Ⅲ)当a>3时,确定f(x)在[
 ,2]上的最大值,g(x)在[
,2]上的最大值,g(x)在[ ,2]上的最小值,要使存在m1,m2∈[
,2]上的最小值,要使存在m1,m2∈[ ,2],使得|f(m1)-g(m2)|<9成立,只需要|f(x)max-g(x)min|<9,即可求得a的取值范围.
,2],使得|f(m1)-g(m2)|<9成立,只需要|f(x)max-g(x)min|<9,即可求得a的取值范围.解答:解:(Ⅰ)求导函数可得f′(x)=1-
 -
- ,…(2分)
,…(2分)由f′(1)=0得b=1-a. …(3分)
(Ⅱ)函数f(x)的定义域为(0,+∞),…(4分)
由(Ⅰ)可得f′(x)=1-
 -
- =
= .
.令f′(x)=0,则x1=1,x2=a-1. …(6分)
因为x=1是f(x)的极值点,所以x1≠x2,即a≠2. …(7分)
所以当a>2时,a-1>1,
| x | (0,1) | 1 | (1,a-1) | a-1 | (a-1,+∞) |
| f′(x) | + | - | + | ||
| f(x) | ↗ | ↘ | ↗ |
当1<a<2时,0<a-1<1,
所以单调递增区间为(0,a-1),(1,+∞),单调递减区间为(a-1,1). …(9分)
(Ⅲ)当a>3时,f(x)在[
 ,1)上为增函数,在(1,2]为减函数,
,1)上为增函数,在(1,2]为减函数,所以f(x)的最大值为f(1)=2-a<0. …(10分)
因为函数g(x)在[
 ,2]上是单调递增函数,所以g(x)的最小值为g(
,2]上是单调递增函数,所以g(x)的最小值为g( )=
)= a2+3>0. …(11分)
a2+3>0. …(11分)所以g(x)>f(x)在[
 ,2]上恒成立. …(12分)
,2]上恒成立. …(12分)要使存在m1,m2∈[
 ,2],使得|f(m1)-g(m2)|<9成立,只需要g(
,2],使得|f(m1)-g(m2)|<9成立,只需要g( )-f(1)<9,即
)-f(1)<9,即 a2+3-(2-a)<9,
a2+3-(2-a)<9,所以-8<a<4. …(13分)
又因为a>3,所以a的取值范围是(3,4). …(14分)
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,解题的关键是正确求导,确定分类标准,利用函数的最值解决恒成立问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
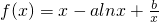 在x=1处取得极值.
在x=1处取得极值. ,使得|f(m1)-g(m2)|<9成立,求a的取值范围.
,使得|f(m1)-g(m2)|<9成立,求a的取值范围. 在x=1处取得极值.
在x=1处取得极值. ,使得|f(m1)-g(m2)|<9成立,求a的取值范围.
,使得|f(m1)-g(m2)|<9成立,求a的取值范围. 在x=1处取得极值.
在x=1处取得极值. ,使得|f(m1)-g(m2)|<9成立,求a的取值范围.
,使得|f(m1)-g(m2)|<9成立,求a的取值范围. 在x=1处取得极值.
在x=1处取得极值. ,使得|f(m1)-g(m2)|<9成立,求a的取值范围.
,使得|f(m1)-g(m2)|<9成立,求a的取值范围.