题目内容
(本小题满分14分)已知抛物线 ,圆
,圆 .
.
(1)在抛物线 上取点
上取点 ,
, 的圆周上取一点
的圆周上取一点 ,求
,求 的最小值;
的最小值;
(2)设
 为抛物线
为抛物线 上的动点,过
上的动点,过 作圆
作圆 的两条切线,交抛物线
的两条切线,交抛物线 于
于 、
、 点,求
点,求 中点
中点 的横坐标的取值范围.
的横坐标的取值范围.
(1)  ; (2)
; (2)  .
.
【解析】
试题分析:(1)  的最小值为
的最小值为 -圆的半径,可设点
-圆的半径,可设点 ,根据两点间距离公式可得
,根据两点间距离公式可得

 ,因而最小值为
,因而最小值为 ;(2) 可设切点
;(2) 可设切点 ,设
,设 ,
, 中点
中点 ,则
,则 将
将 与
与 的方程联立消
的方程联立消 得
得 ,可解出
,可解出 ,则
,则 ,利用点到直线距离公式
,利用点到直线距离公式 ,解得
,解得 ,
,
得到 ,再通过
,再通过 ,分析出
,分析出 ,即可.
,即可.
试题解析: (1).设 ,则
,则 ,
,
则 1分
1分

 ,当且仅当
,当且仅当 是取等号 3分
是取等号 3分

 的最小值为
的最小值为 的最小值减
的最小值减 ,为
,为 5分
5分
(2). 由题设知,切线与 轴不垂直,
轴不垂直,


 ,
, 设切线
设切线
设 ,
, 中点
中点 ,则
,则
将 与
与 的方程联立消
的方程联立消 得
得
即 得
得 (舍)或
(舍)或
设二切线的斜率为 ,则
,则 ,
,

 8分
8分
又 到
到 的距离为1,有
的距离为1,有 ,
,
两边平方得 9分
9分
则 是
是 的二根,则
的二根,则 10分
10分
则

 11分
11分

 在
在 上为增函数
上为增函数

 ,
, 


 13分
13分

 的范围是
的范围是 14分
14分
考点:1、两点间、点到直线的距离公式;2、曲线的切线的有关性质;3、综合分析能力.

练习册系列答案
相关题目
 的展开式中,记
的展开式中,记 项的系数为f(
项的系数为f( ,
, ),则f(3,0)+f(2,1)+f(1,2)+f(0,3) = .
),则f(3,0)+f(2,1)+f(1,2)+f(0,3) = .  ,高为
,高为 的正四棱锥的侧面积为 .
的正四棱锥的侧面积为 . 在点
在点 处的切线方程为 .
处的切线方程为 .  B.
B.
 D.
D.
 内接于圆
内接于圆 ,
, 与圆
与圆 相切于点
相切于点 ,
, ,
, 为
为 的中点,
的中点, ,
, ,
, ,则
,则 .
. 
 对于
对于 ,
, ,定义
,定义 与
与 的差为
的差为 ,定义
,定义 .对于
.对于 ,则下列结论中一定成立的是( )
,则下列结论中一定成立的是( ) B.
B. 
 D.
D. 
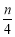 ], Sn为数列{an}的前n项和,则S8= ,S4n= .
], Sn为数列{an}的前n项和,则S8= ,S4n= . ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的范围为_________.
的范围为_________.