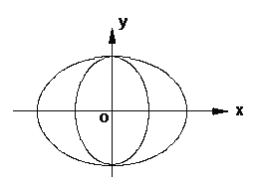
题目内容
【题目】如图，曲线
由两个椭圆
：
和椭圆
：
组成，当
成等比数列时，称曲线为“猫眼曲线”.
（1）若猫眼曲线过点
，且的公比为
，求猫眼曲线的方程；
（2）对于题（1）中的求猫眼曲线，任作斜率为
且不过原点的直线与该曲线相交，交椭圆所得弦的中点为M，交椭圆所得弦的中点为N，求证：
为与
无关的定值；
（3）若斜率为
的直线
为椭圆的切线，且交椭圆于点
，
为椭圆上的任意一点（点与点不重合），求
面积的最大值.
【答案】（1）
，
（2）见解析（3）见解析
【解析】
由题意知
，
，从而求猫眼曲线
的方程；
设交点
，
，从而可得
，联立方程化简可得
，
；从而解得
设直线l的方程为
，联立方程化简
，从而可得
，同理可得
，从而利用两平行线间距离表示三角形的高，再求
；从而求最大面积．
（1），
，
，；
（2）设斜率为
的直线交椭圆
于点
，线段
中点
由
，得
存在且
，
，且
，即
同理，
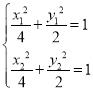得证
（3）设直线
的方程为
，
，
， 
，
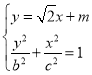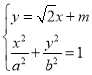两平行线间距离：
的面积最大值为
练习册系列答案
阅读快车系列答案
相关题目
