题目内容
二次函数y=x2的图角的焦点坐标是
- A.(
 )
) - B.
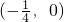
- C.

- D.

A
分析:二次函数y=x2的解析式化为 x2=y,求出 的值,判断焦点位置,从而写出焦点坐标.
的值,判断焦点位置,从而写出焦点坐标.
解答:二次函数y=x2的解析式化为 x2=y,
故 p= ,
, =
= ,再由抛物线的焦点在y轴的正半轴上,
,再由抛物线的焦点在y轴的正半轴上,
可得焦点坐标是(0, ),
),
故选:A.
点评:本题主要考查抛物线的标准方程,以及简单性质的应用,属于基础题.
分析:二次函数y=x2的解析式化为 x2=y,求出
 的值,判断焦点位置,从而写出焦点坐标.
的值,判断焦点位置,从而写出焦点坐标.解答:二次函数y=x2的解析式化为 x2=y,
故 p=
 ,
, =
= ,再由抛物线的焦点在y轴的正半轴上,
,再由抛物线的焦点在y轴的正半轴上,可得焦点坐标是(0,
 ),
),故选:A.
点评:本题主要考查抛物线的标准方程,以及简单性质的应用,属于基础题.

练习册系列答案
相关题目
将二次函数y=x2的图象按向量a平移后,得到的图象与一次函数y=2x-5的图象只有一个公共点(3,1),则向量
=( )
| a |
| A、(2,0) |
| B、(2,1) |
| C、(3,0) |
| D、(3,1) |
 =( )
=( )