题目内容
19．三个圆有相同的半径，都是3，圆心分别为（14，92）、（17，76）和（19，84）．一条直线通过点（17，76），且位于它同一侧的三个圆各部分的面积之和等于另一侧三个圆各部分的面积之和，那么这条直线的斜率的绝对值为$\frac{8}{5}$或24．分析 设出直线方程，利用圆心到直线的距离相等，建立方程，即可得出结论．
解答 解：设直线的方程为y-76=k（x-17），即kx-y-17k+76=0，
∵一条直线通过点（17，76），且位于它同一侧的三个圆各部分的面积之和等于另一侧三个圆各部分的面积之和，
∴$\frac{|14k-92-17k+76|}{\sqrt{{k}^{2}+1}}$=$\frac{|19k-84-17k+76|}{\sqrt{{k}^{2}+1}}$，
∴k=-$\frac{8}{5}$或k=-24，
∴条直线的斜率的绝对值为$\frac{8}{5}$或24．
故答案为：$\frac{8}{5}$或24．
点评 本题考查直线与圆的位置关系，考查点到直线的距离公式的运用，属于中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
10．
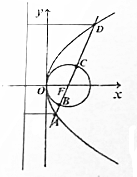如图，抛物线：y2=4mx（m＞0）和圆：x2+y2-2mx=0，直线l经过抛物线的焦点，依次交抛物线，圆于A，B，C，D四点，|AB|•|CD|=2，则m的值为（ ）
如图，抛物线：y2=4mx（m＞0）和圆：x2+y2-2mx=0，直线l经过抛物线的焦点，依次交抛物线，圆于A，B，C，D四点，|AB|•|CD|=2，则m的值为（ ）| A． | 2 | B． | $\sqrt{3}$ | C． | $\sqrt{2}$ | D． | 1 |
7．为了分析某次考试数学成绩情况，用简单随机抽样从某班中抽取40名学生的成绩作为样本，得到频率分布表如表：
（Ⅰ）求样本频率分布表中a，b的值，并根据上述频率分布表，在答题卡中作出样本频率分布直方图；
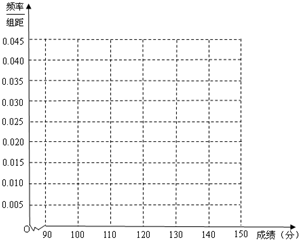
（Ⅱ）用样本估计总体，估计这个班这次数学成绩的平均数．（同一组中的数据用该组区间的中点值作代表）
| 分数 | [90，100） | [100，110） | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 2 | 8 | 12 | a | 6 | 2 |
| 频率 | 0.05 | 0.20 | 0.30 | b | 0.15 | 0.05 |
（Ⅱ）用样本估计总体，估计这个班这次数学成绩的平均数．（同一组中的数据用该组区间的中点值作代表）
4．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F作渐近线的垂线，设垂足为P（P为第一象限的点），延长FP交抛物线y2=2px（p＞0）于点Q，其中该双曲线与抛物线有一个共同的焦点，若$\overrightarrow{OP}$=$\frac{1}{2}$（$\overrightarrow{OF}$+$\overrightarrow{OQ}$），则双曲线的离心率的平方为（ ）
| A． | $\sqrt{5}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | $\sqrt{5}$+1 | D． | $\frac{\sqrt{5}+1}{2}$ |